23. (10分)定义:若两个三角形中,有两组边对应相等且其中一组等边所对的角对应相等,但不是全等三角形,我们就称这两个三角形为“融通三角形”,相等的边所对的相等的角称为“融通角”.
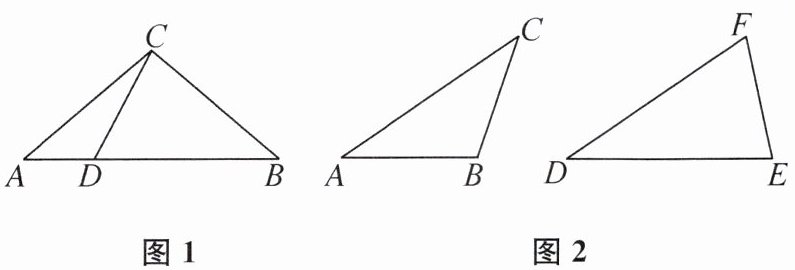
(1) 如图1,在△ABC中,CA= CB,D是AB上任意一点,则△ACD与△BCD____“融通三角形”(填“是”或“不是”).
(2) 如图2,△ABC与△DEF是“融通三角形”,其中∠A= ∠D,AC= DF,BC= EF,求证:∠B+∠E= 180°.
(1)
(2)
(1) 如图1,在△ABC中,CA= CB,D是AB上任意一点,则△ACD与△BCD____“融通三角形”(填“是”或“不是”).
(2) 如图2,△ABC与△DEF是“融通三角形”,其中∠A= ∠D,AC= DF,BC= EF,求证:∠B+∠E= 180°.

(1)
是
(2)
证明:在线段DE上取一点G,使DG=AB,连接FG.因为AC=DF,∠A=∠D,所以△ABC≌△DGF(SAS),所以BC=GF,∠B=∠DGF.因为BC=EF,所以GF=EF,所以∠E=∠FGE.因为∠DGF+∠FGE=180°,所以∠B+∠E=180°.
答案:
(1)是
(2)证明:在线段DE上取一点G,使DG=AB,连接FG.因为AC=DF,∠A=∠D,所以△ABC≌△DGF(SAS),所以BC=GF,∠B=∠DGF.因为BC=EF,所以GF=EF,所以∠E=∠FGE.因为∠DGF+∠FGE=180°,所以∠B+∠E=180°.
(2)证明:在线段DE上取一点G,使DG=AB,连接FG.因为AC=DF,∠A=∠D,所以△ABC≌△DGF(SAS),所以BC=GF,∠B=∠DGF.因为BC=EF,所以GF=EF,所以∠E=∠FGE.因为∠DGF+∠FGE=180°,所以∠B+∠E=180°.
24. (10分)如图,在△ABC中,AC= BC,∠ACB= 90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD的延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.
(1) 线段BE与线段AD有怎样的数量关系? 请说明理由.
(2) 判断△BEG的形状,并说明理由.
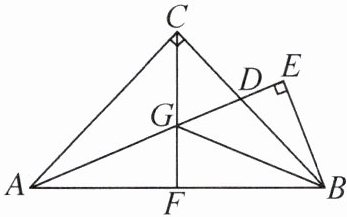
(1) 线段BE与线段AD有怎样的数量关系? 请说明理由.
(2) 判断△BEG的形状,并说明理由.

答案:
(1)BE=$\frac{1}{2}$AD.理由如下:延长AC,BE交于点H.易证△AEH≌△AEB,所以BE=HE=$\frac{1}{2}$BH.因为∠ACB=90°,所以∠BCH=180° - ∠ACB=90°=∠ACD,所以∠CBH=90° - ∠H=∠CAD.又因为AC=BC,所以△BCH≌△ACD,所以AD=BH,所以BE=$\frac{1}{2}$AD.
(2)△BEG是等腰直角三角形.理由如下:因为F为AB的中点,所以AF=BF.又因为AC=BC,所以CF垂直平分AB.因为点G在CF上,所以AG=BG,所以∠GAB=∠GBA.由条件,得∠CAB=∠CBA=45°.因为AD平分∠BAC,所以∠GBA=∠GAB=22.5°,∠EGB=∠GAB+∠GBA=45°.因为∠BEG=90°,所以∠EBG=45°=∠EGB,所以EG=EB,所以△BEG是等腰直角三角形.
(2)△BEG是等腰直角三角形.理由如下:因为F为AB的中点,所以AF=BF.又因为AC=BC,所以CF垂直平分AB.因为点G在CF上,所以AG=BG,所以∠GAB=∠GBA.由条件,得∠CAB=∠CBA=45°.因为AD平分∠BAC,所以∠GBA=∠GAB=22.5°,∠EGB=∠GAB+∠GBA=45°.因为∠BEG=90°,所以∠EBG=45°=∠EGB,所以EG=EB,所以△BEG是等腰直角三角形.
查看更多完整答案,请扫码查看


