《2025年一遍过五年级数学上册苏教版》

1 四边形ABCD中,M为AB的中点,N为CD的中点。已知四边形ABCD的面积是80平方厘米,阴影部分BNDM的面积是多少平方厘米？ 

答案：
80÷2=40(平方厘米)
答:阴影部分BNDM的面积是40平方厘米。
解析　如图，图中阴影部分BNDM是一个不规则的四边形，不能直接求出它的面积。连接BD,将四边形ABCD分成两个三角形。在三角形ABD和三角形BDC中，由于M、N分别是AB、CD的中点，根据等底等高三角形面积相等的道理，可知$S_{三角形AMD}=S_{三角形MBD}$，$S_{三角形DNB}=S_{三角形CNB}$。所以阴影部分的面积与空白部分的两个三角形的面积之和相等，都是四边形ABCD的面积的一半。
　　　　　

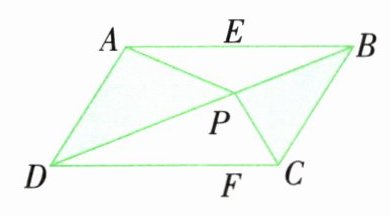
2 如图,平行四边形的面积是50平方厘米,P是其中任意一点,求阴影部分的面积。 视频讲解

答案：
50÷2=25(平方厘米)
答:阴影部分的面积是25平方厘米。
解析　如图，过点P作平行四边形的高，两个空白三角形的面积之和为AB×EP÷2+CD×PF÷2=AB×(EP+PF)÷2=AB×EF÷2，所以空白三角形面积之和与阴影三角形面积之和相等，都等于50÷2=25(平方厘米)。
　　　　　

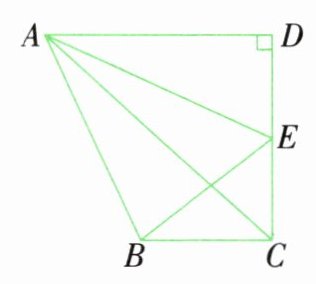
3 如图,已知梯形ABCD的面积是13平方厘米,三角形ADE的面积是4平方厘米,E是CD的中点,三角形BCE的面积是多少？

答案： 三角形ABC的面积:13 - 4 - 4=5(平方厘米)
三角形BCE的面积:5÷2=2.5(平方厘米)
答:三角形BCE的面积是2.5平方厘米。
解析　E是CD的中点，所以$S_{三角形ADE}=S_{三角形AEC}$，所以$S_{三角形ABC}=13 - 4 - 4=5$平方厘米。$S_{三角形ABC}=BC×CD÷2=BC×CE×2÷2=2×(BC×CE÷2)=2×S_{三角形BCE}$，所以$S_{三角形BCE}=5÷2=2.5$平方厘米。