9. 下列操作导致的结果分析不正确的是 (
A.量筒测量液体的体积时,若视线是俯视的,则测得的体积比液体的真实体积要大
B.一把刻度尺的刻度比标准刻度间隔大些,则用这把刻度尺测得的数值比真实值要小
C.用累积法测细金属丝的直径时,若绕线时没有紧密,则测量值比真实值要大
D.用同一金属刻度尺在冬天和夏天测同一物体的长度时,夏天的测量值可能比冬天的要大
D
)A.量筒测量液体的体积时,若视线是俯视的,则测得的体积比液体的真实体积要大
B.一把刻度尺的刻度比标准刻度间隔大些,则用这把刻度尺测得的数值比真实值要小
C.用累积法测细金属丝的直径时,若绕线时没有紧密,则测量值比真实值要大
D.用同一金属刻度尺在冬天和夏天测同一物体的长度时,夏天的测量值可能比冬天的要大
答案:
【解析】:
本题主要考查科学测量中的误差分析,涉及量筒、刻度尺的使用以及累积法的应用,还有温度对测量结果的影响。
A选项:当使用量筒测量液体体积时,如果视线是俯视的,由于视线的斜射,会使得读得的体积数值偏大,即测得的体积比液体的真实体积要大。故A选项正确。
B选项:如果刻度尺的刻度比标准刻度间隔大些,那么在使用这把刻度尺进行测量时,由于每一格代表的长度实际上比标准的大,所以测得的数值会比真实值小。故B选项正确。
C选项:累积法是一种通过测量部分来推算整体的方法。在用累积法测细金属丝的直径时,如果绕线时没有紧密,那么测量的总长度会偏大,由于是通过总长度除以匝数来得到直径的,所以测量值也会偏大。故C选项正确。
D选项:金属具有热胀冷缩的性质。在夏天,由于温度较高,金属刻度尺会膨胀,使得每一格代表的实际长度变长。因此,用膨胀的刻度尺测量物体的长度时,得到的测量值会比用同一把刻度尺在冬天(温度较低,刻度尺收缩)时测量的值要小。故D选项的描述是错误的。
【答案】:D
本题主要考查科学测量中的误差分析,涉及量筒、刻度尺的使用以及累积法的应用,还有温度对测量结果的影响。
A选项:当使用量筒测量液体体积时,如果视线是俯视的,由于视线的斜射,会使得读得的体积数值偏大,即测得的体积比液体的真实体积要大。故A选项正确。
B选项:如果刻度尺的刻度比标准刻度间隔大些,那么在使用这把刻度尺进行测量时,由于每一格代表的长度实际上比标准的大,所以测得的数值会比真实值小。故B选项正确。
C选项:累积法是一种通过测量部分来推算整体的方法。在用累积法测细金属丝的直径时,如果绕线时没有紧密,那么测量的总长度会偏大,由于是通过总长度除以匝数来得到直径的,所以测量值也会偏大。故C选项正确。
D选项:金属具有热胀冷缩的性质。在夏天,由于温度较高,金属刻度尺会膨胀,使得每一格代表的实际长度变长。因此,用膨胀的刻度尺测量物体的长度时,得到的测量值会比用同一把刻度尺在冬天(温度较低,刻度尺收缩)时测量的值要小。故D选项的描述是错误的。
【答案】:D
10. 小强同学用量筒量取液体,将量筒放好后,先俯视量筒内液体凹液面的最低处,读数为 $21mL$,倒出部分液体后,仰视凹液面的最低处,读数为 $8mL$,则该同学实际倒出液体的体积 (
A.大于 $13mL$
B.等于 $13mL$
C.小于 $13mL$
D.无法判断
C
)A.大于 $13mL$
B.等于 $13mL$
C.小于 $13mL$
D.无法判断
答案:
【解析】:
此题主要考查了量筒的使用方法和读数时的注意事项。在使用量筒时,读数时不能仰视或俯视,视线要与凹液面最低处保持水平。如果仰视或俯视读数,会造成读数不准确,从而影响实验结果。对于此题,先俯视读数为$21mL$,由于俯视会使得读数偏大,所以实际液体体积应小于$21mL$;后仰视读数为$8mL$,由于仰视会使得读数偏小,所以实际剩余液体体积应大于$8mL$。因此,该同学实际倒出的液体体积应小于$21 - 8 = 13mL$。
【答案】:C
此题主要考查了量筒的使用方法和读数时的注意事项。在使用量筒时,读数时不能仰视或俯视,视线要与凹液面最低处保持水平。如果仰视或俯视读数,会造成读数不准确,从而影响实验结果。对于此题,先俯视读数为$21mL$,由于俯视会使得读数偏大,所以实际液体体积应小于$21mL$;后仰视读数为$8mL$,由于仰视会使得读数偏小,所以实际剩余液体体积应大于$8mL$。因此,该同学实际倒出的液体体积应小于$21 - 8 = 13mL$。
【答案】:C
11. 某同学用 $20mL$ 的量筒用排水法收集气体到一定的时候,按右图中的方式读数为 $4.0mL$,他实际收集到的气体体积应该是 (
A.大于 $4mL$
B.小于 $4mL$
C.大于 $16mL$
D.小于 $16mL$
D
)A.大于 $4mL$
B.小于 $4mL$
C.大于 $16mL$
D.小于 $16mL$
答案:
【解析】:
本题考查量筒的正确读数方法以及排水法收集气体时量筒内液体的体积变化。
在使用量筒测量液体体积时,正确的读数方法是视线与量筒内液体凹液面的最低处保持水平。
如果仰视读数,读数会小于实际体积;如果俯视读数,读数会大于实际体积。
题目中,同学按图中方式读数为$4.0mL$,从图中可以看出,这种读数方式是俯视读数,所以实际液体体积应大于$4.0mL$。
因为量筒的规格是$20mL$,用排水法收集气体,量筒内原有$20mL$水,现在读数偏小,实际水体积大于$4.0mL$,那么收集到的气体体积就应该是量筒内原有的$20mL$水减去实际水的体积,所以实际收集到的气体体积小于$16mL$。
【答案】:D
本题考查量筒的正确读数方法以及排水法收集气体时量筒内液体的体积变化。
在使用量筒测量液体体积时,正确的读数方法是视线与量筒内液体凹液面的最低处保持水平。
如果仰视读数,读数会小于实际体积;如果俯视读数,读数会大于实际体积。
题目中,同学按图中方式读数为$4.0mL$,从图中可以看出,这种读数方式是俯视读数,所以实际液体体积应大于$4.0mL$。
因为量筒的规格是$20mL$,用排水法收集气体,量筒内原有$20mL$水,现在读数偏小,实际水体积大于$4.0mL$,那么收集到的气体体积就应该是量筒内原有的$20mL$水减去实际水的体积,所以实际收集到的气体体积小于$16mL$。
【答案】:D
12. 用材料甲制成的刻度尺去测量用材料乙制成的物体的长度。在 $5^{\circ}C$ 时测得的长度为 $L_{1}$,在 $30^{\circ}C$ 时测得的长度为 $L_{2}$。如果两次的测量方法都正确,且 $L_{1} > L_{2}$。则下列说法中正确的是 (
A.甲、乙两种材料膨胀程度不同,且材料乙的膨胀程度大
B.如果在 $15^{\circ}C$ 时取甲、乙两材料的长度均是 $1m$,则降低相同温度后甲的长度大于乙的长度
C.如果在 $15^{\circ}C$ 时取甲、乙两材料的长度均是 $1m$,则升高相同温度后甲的长度大于乙的长度
D.以上三种情况都不对
C
)A.甲、乙两种材料膨胀程度不同,且材料乙的膨胀程度大
B.如果在 $15^{\circ}C$ 时取甲、乙两材料的长度均是 $1m$,则降低相同温度后甲的长度大于乙的长度
C.如果在 $15^{\circ}C$ 时取甲、乙两材料的长度均是 $1m$,则升高相同温度后甲的长度大于乙的长度
D.以上三种情况都不对
答案:
解:在5℃时,刻度尺和物体长度分别为$L_{甲1}$、$L_{乙1}$,测量值$L_{1}=\frac{L_{乙1}}{L_{甲1}}× 刻度间隔$;30℃时,刻度尺和物体长度分别为$L_{甲2}$、$L_{乙2}$,测量值$L_{2}=\frac{L_{乙2}}{L_{甲2}}× 刻度间隔$。因$L_{1}>L_{2}$,且温度升高,所以$\frac{L_{乙1}}{L_{甲1}}>\frac{L_{乙2}}{L_{甲2}}$,即$\frac{L_{乙2}}{L_{乙1}}<\frac{L_{甲2}}{L_{甲1}}$,说明甲膨胀程度大于乙。
A. 甲膨胀程度大,A错误。
B. 降低相同温度,甲收缩程度大,原长均1m,甲长度小于乙,B错误。
C. 升高相同温度,甲膨胀程度大,原长均1m,甲长度大于乙,C正确。
答案:C
A. 甲膨胀程度大,A错误。
B. 降低相同温度,甲收缩程度大,原长均1m,甲长度小于乙,B错误。
C. 升高相同温度,甲膨胀程度大,原长均1m,甲长度大于乙,C正确。
答案:C
13. 桌面上有一个量筒和一个量杯,量程都是 $100mL$,设杯底到最大量程的高度都是 $h$,如果倒入 $25mL$ 的液体,对量杯而言,液面的高度将
大于
(填“大于”“小于”或“等于”,下同)$h/4$;但是小科在用量筒量取液体的过程中俯视凹液面最低处,则实际量取的液体体积小于
$25mL$。
答案:
【解析】:
本题主要考查量筒和量杯的形状特点以及量筒的读数方式。
对于量杯,其形状是上宽下窄,因此在倒入相同体积的液体时,液面在量杯中的高度会比在量筒中的高度要高。
对于量筒的读数,如果俯视凹液面最低处,由于视线的折射和视觉错觉,会使得读数偏大,而实际量取的液体体积会偏小。
首先,我们分析量杯的情况。
由于量杯的形状是上宽下窄,当倒入$25mL$液体时,液面的高度会大于量杯高度的四分之一,即大于 $h/4$。
其次,我们分析量筒的情况。
小科在用量筒量取液体时,如果俯视凹液面最低处,那么由于视线的折射,他会看到一个比实际液面位置更高的虚像,从而导致他读取的数值比实际值偏大。
因此,他实际量取的液体体积会小于$25mL$。
【答案】:
大于;小于。
本题主要考查量筒和量杯的形状特点以及量筒的读数方式。
对于量杯,其形状是上宽下窄,因此在倒入相同体积的液体时,液面在量杯中的高度会比在量筒中的高度要高。
对于量筒的读数,如果俯视凹液面最低处,由于视线的折射和视觉错觉,会使得读数偏大,而实际量取的液体体积会偏小。
首先,我们分析量杯的情况。
由于量杯的形状是上宽下窄,当倒入$25mL$液体时,液面的高度会大于量杯高度的四分之一,即大于 $h/4$。
其次,我们分析量筒的情况。
小科在用量筒量取液体时,如果俯视凹液面最低处,那么由于视线的折射,他会看到一个比实际液面位置更高的虚像,从而导致他读取的数值比实际值偏大。
因此,他实际量取的液体体积会小于$25mL$。
【答案】:
大于;小于。
14. 有下列器材:a. 白纸条;b. 细线;c. 大头针;d. 刻度尺;e. 量筒;f. 圆柱体。若要测出圆柱体的周长,应选用的器材是 (
A.adef
B.acde
C.acdf
D.abdf
C
)A.adef
B.acde
C.acdf
D.abdf
答案:
【解析】:
本题主要考查如何使用给定器材测量圆柱体的周长。解题的关键在于理解并应用“替代法”或“化曲为直法”来间接测量圆柱体的周长。我们需要分析每个器材的作用以及它们如何组合起来达到测量目的。
a. 白纸条:可以用来紧贴圆柱体,并通过标记来“替代”或“化曲为直”圆柱体的周长。
b. 细线:同样可以用来紧贴圆柱体,并通过测量细线的长度来间接测量圆柱体的周长。但在此题中,由于已经有了白纸条作为更直接的“化曲为直”工具,细线可能不是必需的,但它仍然是一个可行的替代方案,特别是如果白纸条不够长或不够灵活时。然而,考虑到题目的选项和常规测量方法,我们主要关注白纸条的使用。
c. 大头针:用于在白纸条上做标记,以便后续测量。它是必需的,因为我们需要知道白纸条上哪一段长度等于圆柱体的周长。
d. 刻度尺:用于测量白纸条上标记段的长度,从而得出圆柱体的周长。它是必需的测量工具。
e. 量筒:用于测量液体的体积,与本题测量圆柱体的周长无关。
f. 圆柱体:显然是本题要测量的对象。
综上所述,为了测量圆柱体的周长,我们需要白纸条(a)来“化曲为直”,大头针(c)来做标记,刻度尺(d)来测量长度,以及圆柱体(f)本身作为测量对象。因此,应选用的器材是a、c、d、f。
【答案】:C
本题主要考查如何使用给定器材测量圆柱体的周长。解题的关键在于理解并应用“替代法”或“化曲为直法”来间接测量圆柱体的周长。我们需要分析每个器材的作用以及它们如何组合起来达到测量目的。
a. 白纸条:可以用来紧贴圆柱体,并通过标记来“替代”或“化曲为直”圆柱体的周长。
b. 细线:同样可以用来紧贴圆柱体,并通过测量细线的长度来间接测量圆柱体的周长。但在此题中,由于已经有了白纸条作为更直接的“化曲为直”工具,细线可能不是必需的,但它仍然是一个可行的替代方案,特别是如果白纸条不够长或不够灵活时。然而,考虑到题目的选项和常规测量方法,我们主要关注白纸条的使用。
c. 大头针:用于在白纸条上做标记,以便后续测量。它是必需的,因为我们需要知道白纸条上哪一段长度等于圆柱体的周长。
d. 刻度尺:用于测量白纸条上标记段的长度,从而得出圆柱体的周长。它是必需的测量工具。
e. 量筒:用于测量液体的体积,与本题测量圆柱体的周长无关。
f. 圆柱体:显然是本题要测量的对象。
综上所述,为了测量圆柱体的周长,我们需要白纸条(a)来“化曲为直”,大头针(c)来做标记,刻度尺(d)来测量长度,以及圆柱体(f)本身作为测量对象。因此,应选用的器材是a、c、d、f。
【答案】:C
15. 一油漆匠给面积为 $12m^{2}$ 的地板刷油漆,用去油漆 $6L$,地板上油漆的平均厚度是
0.5mm
。
答案:
【解析】:本题主要考察的是体积、面积和厚度之间的关系。根据体积的计算公式$V = S × h$,其中$V$是体积,$S$是面积,$h$是高度(或厚度)。题目中给出了油漆的体积和地板的面积,我们可以通过这个公式来求解油漆的平均厚度。
将已知的$V = 6L = 6 × 10^{-3}m^{3}$和$S = 12m^{2}$代入公式,解出$h$,即油漆的平均厚度。
计算过程为:$h = \frac{V}{S} = \frac{6 × 10^{-3}m^{3}}{12m^{2}} = 0.0005m = 0.5mm$。
【答案】:$0.5mm$。
将已知的$V = 6L = 6 × 10^{-3}m^{3}$和$S = 12m^{2}$代入公式,解出$h$,即油漆的平均厚度。
计算过程为:$h = \frac{V}{S} = \frac{6 × 10^{-3}m^{3}}{12m^{2}} = 0.0005m = 0.5mm$。
【答案】:$0.5mm$。
16. 玩游戏用的游戏币(放入水中会沉于水中),其形状类似于圆柱,其表面凹凸不平,如图所示。学习了测量新知识的小缙特别想知道一枚游戏币的直径与体积是多大,于是马上进行了测量。
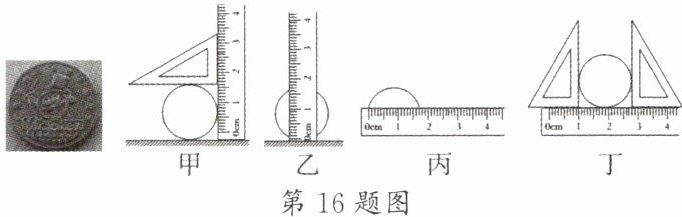
(1)经过思考,他设计了以上四种测圆柱直径的方法,你认为图____
(2)采用了正确方法后,小缙进行了五次测量,结果分别是 $2.20cm$、$2.21cm$、$2.95cm$、$2.20cm$、$2.21cm$,你认为他得到的结果是____

(1)经过思考,他设计了以上四种测圆柱直径的方法,你认为图____
甲
是正确的。(2)采用了正确方法后,小缙进行了五次测量,结果分别是 $2.20cm$、$2.21cm$、$2.95cm$、$2.20cm$、$2.21cm$,你认为他得到的结果是____
2.21cm
。
答案:
【解析】:
(1) 甲图:直尺与三角板垂直放置且零刻度与圆柱底部对齐,能准确测量出直径,该方法正确;乙图:直尺零刻度未与圆柱底部对齐,测量结果会偏小,该方法错误;丙图:直尺没有与圆柱直径方向对齐,无法准确测量直径,该方法错误;丁图:两个三角板的斜边与圆柱相切,不能准确确定直径位置,该方法错误。
从甲图可以看出,是用“卡测法”测圆柱体直径,圆柱体左侧与$1.00cm$对齐,右侧与$3.20cm$对齐,所以直径为$d=3.20cm - 1.00cm = 2.20cm$。
(2) 五次测量数据中,$2.95cm$与其他数据相差较大,属于错误数据,应舍去。取其余四次正确测量值的平均值作为测量结果,即$d=\frac{2.20cm + 2.21cm + 2.20cm + 2.21cm}{4}=2.205cm\approx2.21cm$。
【答案】:
(1) 甲
(2) $2.21cm$
(1) 甲图:直尺与三角板垂直放置且零刻度与圆柱底部对齐,能准确测量出直径,该方法正确;乙图:直尺零刻度未与圆柱底部对齐,测量结果会偏小,该方法错误;丙图:直尺没有与圆柱直径方向对齐,无法准确测量直径,该方法错误;丁图:两个三角板的斜边与圆柱相切,不能准确确定直径位置,该方法错误。
从甲图可以看出,是用“卡测法”测圆柱体直径,圆柱体左侧与$1.00cm$对齐,右侧与$3.20cm$对齐,所以直径为$d=3.20cm - 1.00cm = 2.20cm$。
(2) 五次测量数据中,$2.95cm$与其他数据相差较大,属于错误数据,应舍去。取其余四次正确测量值的平均值作为测量结果,即$d=\frac{2.20cm + 2.21cm + 2.20cm + 2.21cm}{4}=2.205cm\approx2.21cm$。
【答案】:
(1) 甲
(2) $2.21cm$
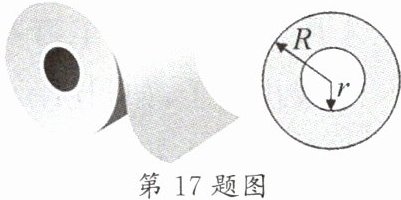
17. 甲、乙两同学想测量一卷筒纸的总长度。考虑到纸筒上绕的纸很长,不可能将纸全部放开拉直了再用尺测量。($\pi$ 取 3)
甲同学的方法是:首先从卷筒纸的标签上了解到,卷筒纸拉开后纸的厚度为 $0.04cm$,然后测出卷筒纸内半径 $r$ 为 $2cm$,外半径 $R$ 为 $6cm$,则卷筒纸的总长度 $L$ 为
乙同学的方法是:首先测出卷筒纸内半径 $r$ 为 $2cm$,外半径 $R$ 为 $6cm$,然后拉开部分卷筒纸测出它的长度为 $L_{0}$ 为 $6.6m$,此时卷筒纸的外半径减小到 $R_{0}(R_{0} = 5cm)$,则卷筒纸的总长度 $L$ 为
甲同学的方法是:首先从卷筒纸的标签上了解到,卷筒纸拉开后纸的厚度为 $0.04cm$,然后测出卷筒纸内半径 $r$ 为 $2cm$,外半径 $R$ 为 $6cm$,则卷筒纸的总长度 $L$ 为
2400
$cm$。乙同学的方法是:首先测出卷筒纸内半径 $r$ 为 $2cm$,外半径 $R$ 为 $6cm$,然后拉开部分卷筒纸测出它的长度为 $L_{0}$ 为 $6.6m$,此时卷筒纸的外半径减小到 $R_{0}(R_{0} = 5cm)$,则卷筒纸的总长度 $L$ 为
1920
$cm$。
答案:
解:甲同学:
卷筒纸的横截面积 $ S = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) $
$ R = 6\ \text{cm} $,$ r = 2\ \text{cm} $,$ \pi = 3 $
$ S = 3×(6^2 - 2^2) = 3×(36 - 4) = 3×32 = 96\ \text{cm}^2 $
纸的厚度 $ d = 0.04\ \text{cm} $,总长度 $ L = \frac{S}{d} = \frac{96}{0.04} = 2400\ \text{cm} $
乙同学:
拉开部分纸的横截面积 $ S_0 = \pi R^2 - \pi R_0^2 = \pi (R^2 - R_0^2) $
$ R = 6\ \text{cm} $,$ R_0 = 5\ \text{cm} $
$ S_0 = 3×(6^2 - 5^2) = 3×(36 - 25) = 3×11 = 33\ \text{cm}^2 $
$ L_0 = 6.6\ \text{m} = 660\ \text{cm} $,纸的厚度 $ d = \frac{S_0}{L_0} = \frac{33}{660} = 0.05\ \text{cm} $
卷筒纸总横截面积 $ S = 96\ \text{cm}^2 $(同甲同学)
总长度 $ L = \frac{S}{d} = \frac{96}{0.05} = 1920\ \text{cm} $
2400;1920
卷筒纸的横截面积 $ S = \pi R^2 - \pi r^2 = \pi (R^2 - r^2) $
$ R = 6\ \text{cm} $,$ r = 2\ \text{cm} $,$ \pi = 3 $
$ S = 3×(6^2 - 2^2) = 3×(36 - 4) = 3×32 = 96\ \text{cm}^2 $
纸的厚度 $ d = 0.04\ \text{cm} $,总长度 $ L = \frac{S}{d} = \frac{96}{0.04} = 2400\ \text{cm} $
乙同学:
拉开部分纸的横截面积 $ S_0 = \pi R^2 - \pi R_0^2 = \pi (R^2 - R_0^2) $
$ R = 6\ \text{cm} $,$ R_0 = 5\ \text{cm} $
$ S_0 = 3×(6^2 - 5^2) = 3×(36 - 25) = 3×11 = 33\ \text{cm}^2 $
$ L_0 = 6.6\ \text{m} = 660\ \text{cm} $,纸的厚度 $ d = \frac{S_0}{L_0} = \frac{33}{660} = 0.05\ \text{cm} $
卷筒纸总横截面积 $ S = 96\ \text{cm}^2 $(同甲同学)
总长度 $ L = \frac{S}{d} = \frac{96}{0.05} = 1920\ \text{cm} $
2400;1920
查看更多完整答案,请扫码查看


