《2025年假期伴你行暑假合肥工业大学出版社八年级数学沪科版》

10. (宜宾模拟)如图,长方体盒子的长、宽、高分别是$12\ \text{cm}$,$8\ \text{cm}$,$30\ \text{cm}$,在$AB的中点C$处有一滴蜜糖,一只小虫从$E处沿盒子表面爬到C$处去吃,求小虫爬行的最短路程.

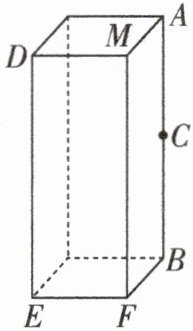
答案：
解: 分为三种情况:
(1) 如图①, 连接 EC. 在 $Rt\triangle EBC$ 中, $EB=12+8=20$ (cm), $BC=\frac{1}{2}×30=15$ (cm). 由勾股定理, 得 $EC=\sqrt{20^{2}+15^{2}}=25$ (cm).
(2) 如图②, 连接 EC. 同理可求 $CE=\sqrt{673}$ cm ＞ 25 cm.
(3) 如图③, 连接 EC. 同理可求 $CE=\sqrt{2953}$ cm ＞ 25 cm. 综上可知, 小虫爬行的最短路程是 25 cm.
　 　

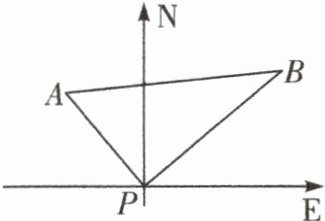
11. (玉林中考)如图,某港口$P$位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行$12海里和16$海里,$1小时后两船分别位于点A$,$B$处,且相距$20$海里,如果知道甲船沿北偏西$40^{\circ}$方向航行,则乙船沿北偏东$50^{\circ}$方向航行.

答案： 北偏东 $50^{\circ}$

12. (盐城期末)如图,南北线$MN$为我国领海线,即$MN$以西为我国领海,以东为公海. 上午$9时50$分,我国反走私艇$A发现正东方向有一走私艇C以13$海里/时的速度偷偷向我领海开来,便立即通知正在$MN线上巡逻的我国反走私艇B$密切注意. 反走私艇$A和走私艇C的距离是13$海里,$A$,$B两艇的距离是5$海里,反走私艇$B和走私艇C的距离是12$海里. 若走私艇$C$的速度不变,最早会在10时41分进入我国领海？

答案： 解: 设 MN 与 AC 相交于点 E, 则 $∠BEC=90^{\circ}$.
$\because AB^{2}+BC^{2}=5^{2}+12^{2}=13^{2}=AC^{2}$, $\therefore \triangle ABC$ 为直角三角形, 且 $∠ABC=90^{\circ}$. $\because MN⊥CE$, 点 E 为 MN 与 AC 的交点, $\therefore$ 走私艇 C 进入我国领海的最短距离是线段 CE 的长. 由 $S_{\triangle ABC}=\frac{1}{2}AB\cdot BC=\frac{1}{2}AC\cdot BE$, 得 $BE=\frac{AB\cdot BC}{AC}=\frac{5×12}{13}=\frac{60}{13}$ (海里). 由 $CE^{2}+BE^{2}=BC^{2}=12^{2}$, 得 $CE=\frac{144}{13}$. $\therefore \frac{144}{13}÷13=\frac{144}{169}≈0.85$ (h) = 51 (min), 9 时 50 分 + 51 分 = 10 时 41 分. 答: 走私艇 C 最早在 10 时 41 分进入我国领海.

13. (青岛中考)如图,三角形纸片$ABC$,$AB = AC$,$\angle BAC = 90^{\circ}$,点$E为AB$中点. 将$\triangle ABC沿过点E$的直线折叠,使点$B与点A$重合,折痕$EF交BC于点F$. 已知$EF = \dfrac{3}{2}$,则$BC$的长是(B)
A.$\dfrac{3\sqrt{2}}{2}$
B.$3\sqrt{2}$
C.3
D.$3\sqrt{3}$

答案： B

14. (杭州模拟)如图,将长$AB = 5\ \text{cm}$,宽$AD = 3\ \text{cm}的矩形纸片ABCD$折叠,使点$A与C$重合,折痕为$EF$,则$AE$长为____3.4$\text{cm}$.

答案： 3.4