《2025年新暑假生活四年级数学人教版》

三、下面是几组小棒的长度,在能拼成三角形的组后面画“√”。
1. 6 cm/6 cm/8 cm(√)
2. 4 cm/4 cm/4 cm(√)
3. 5 cm/12 cm/13 cm(√)
4. 2 cm/6 cm/3 cm()

答案： 1. √ 2. √ 3. √

四、请说明哪种围篱笆的方法更牢固。

答案： 第一种更牢固。

五、判断(对的打“√”,错的打“×”)。
1. 直角三角形只有两个锐角。 (√)
2. 如果一个三角形中最大的角大于90°,那么这个三角形一定是钝角三角形。 (√)
3. 一个三角形不是锐角三角形就是直角三角形。 (×)
4. 有两个角是锐角的三角形是锐角三角形。 (×)

答案： 1. √ 2. √ 3. × 4. ×

六、看下图,从左到右分别是三条线路,从起点到终点走哪条路最近？

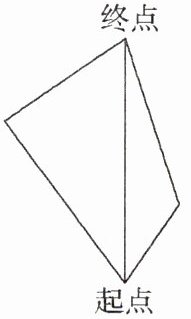
答案： 走中间的路最近。

从3根6 cm、1根8 cm、1根10 cm、1根12 cm长的小棒中,任取3根,能摆几个不同的三角形？它们分别是什么三角形？

答案： 【解析】：根据三角形的特性：任意两边之和大于第三边，任意两边之差小于第三边来判断能否组成三角形。
取$3$根$6cm$的小棒，因为$6 + 6＞6$，$6 - 6＜6$，可以组成三角形，三边相等，是等边三角形。
取$2$根$6cm$和$1$根$8cm$的小棒，$6+6 = 12＞8$，$8 - 6 = 2＜6$，可以组成三角形，有两条边相等，是等腰三角形。
取$2$根$6cm$和$1$根$10cm$的小棒，$6 + 6=12＞10$，$10 - 6 = 4＜6$，可以组成三角形，有两条边相等，是等腰三角形。
取$2$根$6cm$和$1$根$12cm$的小棒，$6+6 = 12$，不满足两边之和大于第三边，不能组成三角形。
取$1$根$6cm$、$1$根$8cm$和$1$根$10cm$的小棒，$6 + 8＞10$，$10 - 6＜8$，$10 - 8＜6$，$8 + 10＞6$，可以组成三角形，三边都不相等，是一般三角形。
取$1$根$6cm$、$1$根$8cm$和$1$根$12cm$的小棒，$6+8＞12$，$12 - 6＜8$，$12 - 8＜6$，$8 + 12＞6$，可以组成三角形，三边都不相等，是一般三角形。
取$1$根$6cm$、$1$根$10cm$和$1$根$12cm$的小棒，$6+10＞12$，$12 - 6＜10$，$12 - 10＜6$，$10 + 12＞6$，可以组成三角形，三边都不相等，是一般三角形。
取$1$根$8cm$、$1$根$10cm$和$1$根$12cm$的小棒，$8 + 10＞12$，$12 - 8＜10$，$12 - 10＜8$，$10 + 12＞8$，可以组成三角形，三边都不相等，是一般三角形。
【答案】：能摆$7$个不同的三角形，分别是：等边三角形（$3$根$6cm$）；等腰三角形（$2$根$6cm$和$1$根$8cm$、$2$根$6cm$和$1$根$10cm$）；一般三角形（$1$根$6cm$、$1$根$8cm$和$1$根$10cm$；$1$根$6cm$、$1$根$8cm$和$1$根$12cm$；$1$根$6cm$、$1$根$10cm$和$1$根$12cm$；$1$根$8cm$、$1$根$10cm$和$1$根$12cm$）。