2025年时习之暑假衔接七年级数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年时习之暑假衔接七年级数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
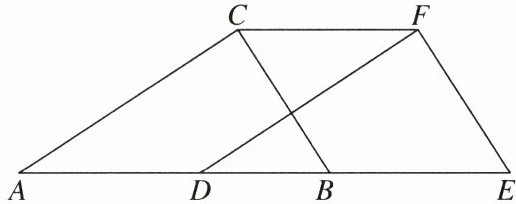
20. (8分)如图,在$\triangle ABC$中,$\angle ACB= 90^{\circ}$,$\angle A= 33^{\circ}$,将$\triangle ABC沿AB方向向右平移得到\triangle DEF$.
(1)试求出$\angle E$的度数;
(2)若$AE= 9cm$,$DB= 2cm$,请求出$CF$的长度.
(1)试求出$\angle E$的度数;
(2)若$AE= 9cm$,$DB= 2cm$,请求出$CF$的长度.

答案:
(1) $ \because $ 在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ \angle A = 33^{\circ} $,$ \therefore \angle CBA = 90^{\circ} - 33^{\circ} = 57^{\circ} $. 由平移得 $ \angle E = \angle CBA = 57^{\circ} $.
(2) 由平移得 $ AD = BE = CF $,$ \because AE = 9 \text{ cm} $,$ DB = 2 \text{ cm} $,$ \therefore AD = BE = \frac{1}{2} × (9 - 2) = 3.5 (\text{cm}) $. $ \therefore CF = 3.5 \text{ cm} $.
(1) $ \because $ 在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ \angle A = 33^{\circ} $,$ \therefore \angle CBA = 90^{\circ} - 33^{\circ} = 57^{\circ} $. 由平移得 $ \angle E = \angle CBA = 57^{\circ} $.
(2) 由平移得 $ AD = BE = CF $,$ \because AE = 9 \text{ cm} $,$ DB = 2 \text{ cm} $,$ \therefore AD = BE = \frac{1}{2} × (9 - 2) = 3.5 (\text{cm}) $. $ \therefore CF = 3.5 \text{ cm} $.
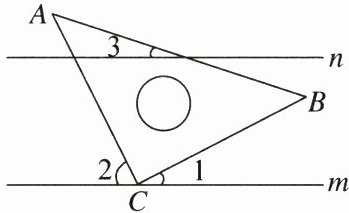
21. (8分)如图,将含有$45^{\circ}角的三角板ABC的直角顶点C放在直线m$上,若$\angle 1= 27^{\circ}$.
(1)求$\angle 2$的度数;
(2)若$\angle 3= 18^{\circ}$,判断直线$n和m$的位置关系,并说明理由.
(1)求$\angle 2$的度数;
(2)若$\angle 3= 18^{\circ}$,判断直线$n和m$的位置关系,并说明理由.

答案:
(1) $ \because \angle 1 + \angle ACB + \angle 2 = 180^{\circ} $,$ \angle 1 = 27^{\circ} $,$ \angle ACB = 90^{\circ} $,$ \therefore \angle 2 = 180^{\circ} - 90^{\circ} - 27^{\circ} = 63^{\circ} $.
(2) $ m // n $. 理由如下:过点 $ B $ 向左作 $ BD // m $,$ \therefore \angle DBC = \angle 1 = 27^{\circ} $. $ \because \angle ABC = 45^{\circ} $,$ \therefore \angle ABD = 45^{\circ} - 27^{\circ} = 18^{\circ} $. 又 $ \because \angle 3 = 18^{\circ} $,$ \therefore \angle 3 = \angle ABD $. $ \therefore BD // n $. $ \therefore m // n $.
(1) $ \because \angle 1 + \angle ACB + \angle 2 = 180^{\circ} $,$ \angle 1 = 27^{\circ} $,$ \angle ACB = 90^{\circ} $,$ \therefore \angle 2 = 180^{\circ} - 90^{\circ} - 27^{\circ} = 63^{\circ} $.
(2) $ m // n $. 理由如下:过点 $ B $ 向左作 $ BD // m $,$ \therefore \angle DBC = \angle 1 = 27^{\circ} $. $ \because \angle ABC = 45^{\circ} $,$ \therefore \angle ABD = 45^{\circ} - 27^{\circ} = 18^{\circ} $. 又 $ \because \angle 3 = 18^{\circ} $,$ \therefore \angle 3 = \angle ABD $. $ \therefore BD // n $. $ \therefore m // n $.
22. (10分)为了解学生使用手机的情况,某学校开展了“手机伴我健康行”主题活动,随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并根据调查结果绘制成如图①②所示的统计图,已知“查资料”的人数是40人.
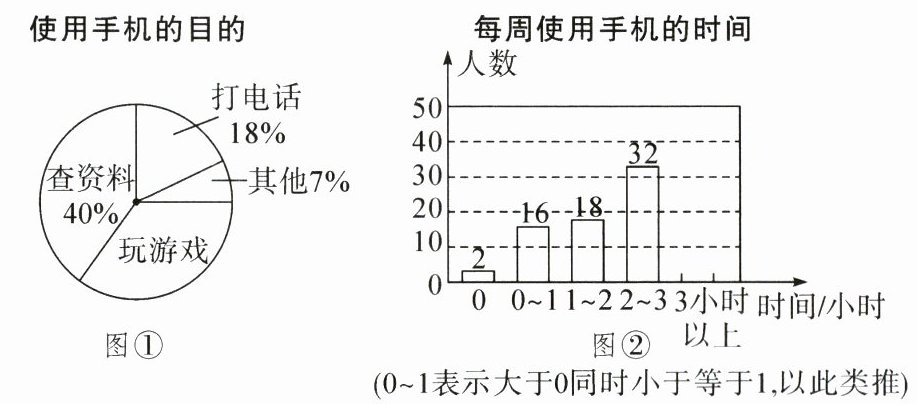
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生4800人,估计每周使用手机的时间在2小时以上(不含2小时)的人数.

请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生4800人,估计每周使用手机的时间在2小时以上(不含2小时)的人数.
答案:
(1) 126
(2) 根据题意得 $ 40 ÷ 40\% = 100 $ (人),$ \therefore 3 $ 小时以上的人数为 $ 100 - (2 + 16 + 18 + 32) = 32 $ (人).
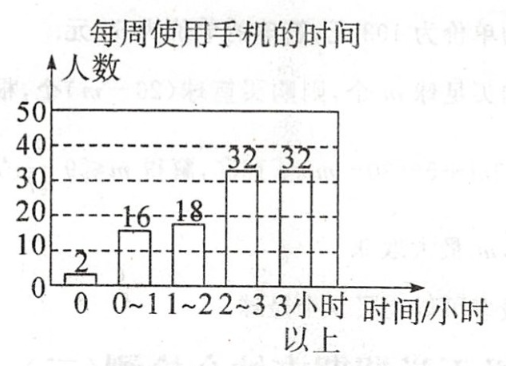
(3) 根据题意得 $ 4800 × \frac{32 + 32}{100} × 100\% = 3072 $ (人),则每周使用手机时间在 2 小时以上(不含 2 小时)的人数约为 3072 人.
(1) 126
(2) 根据题意得 $ 40 ÷ 40\% = 100 $ (人),$ \therefore 3 $ 小时以上的人数为 $ 100 - (2 + 16 + 18 + 32) = 32 $ (人).

(3) 根据题意得 $ 4800 × \frac{32 + 32}{100} × 100\% = 3072 $ (人),则每周使用手机时间在 2 小时以上(不含 2 小时)的人数约为 3072 人.
查看更多完整答案,请扫码查看


