《2025年时习之暑假衔接七年级数学人教版》

15. 小芳准备用30元钱买钢笔和笔记本,已知一支钢笔4.5元,一本笔记本3元,她买了5本笔记本,则她最多还可以买______支钢笔.

答案： 3

16. 如图,用8块相同的小长方形瓷砖拼成一个大长方形贴在墙面上,则每块小长方形瓷砖的面积是______$cm^{2}$.

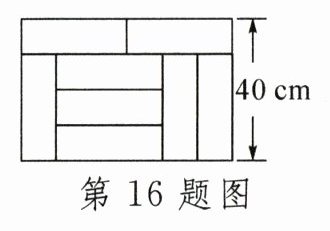
答案： 300

17. (8分)解下列方程组或不等式组：
(1)$\left\{\begin{array}{l}3x-2y= 5,\\ 2x+7y= -5;\end{array} \right.$
(2)$\left\{\begin{array}{l}3(x-2)\geqslant x-4,\\ \frac{2x+1}{3}＞x-1.\end{array} \right.$

答案：
(1)
解：
给$3x - 2y = 5$两边同时乘以$7$，得$21x-14y = 35$ 
给$2x + 7y = - 5$两边同时乘以$2$，得$4x + 14y = - 10$ 
将上述两个新方程相加消去$y$：
$(21x-14y)+(4x + 14y)=35+(-10)$
$21x-14y + 4x + 14y=35 - 10$
$25x=25$
解得$x = 1$。
把$x = 1$代入$3x - 2y = 5$，得$3×1-2y = 5$，即$3-2y = 5$。
移项可得$-2y=5 - 3$，即$-2y = 2$，解得$y=-1$。
所以方程组的解为$\begin{cases}x = 1 \\y = - 1 \\\end{cases}$。
(2)
解：
解不等式$3(x - 2)\geqslant x - 4$：
去括号得$3x-6\geqslant x - 4$。
移项得$3x-x\geqslant - 4 + 6$。
合并同类项得$2x\geqslant2$，解得$x\geqslant1$。
解不等式$\frac{2x + 1}{3}\gt x - 1$：
去分母得$2x + 1\gt 3(x - 1)$。
去括号得$2x + 1\gt 3x - 3$。
移项得$2x-3x\gt - 3 - 1$。
合并同类项得$-x\gt - 4$，解得$x\lt4$。
所以不等式组的解集为$1\leqslant x\lt4$。
综上，答案依次为：$(1)$$\boldsymbol{\begin{cases}x = 1 \\y = - 1 \\\end{cases}}$；$(2)$$\boldsymbol{1\leqslant x\lt4}$。

18. (8分)已知$x^{2}= 81$,$y= \sqrt[3]{-27}$,求$x+y$的值.

答案： 依题意得 $ x = \pm 9 $，$ y = -3 $，故 $ x + y = 6 $ 或 $ -12 $.

19. (8分)关于$x$,$y的方程组\left\{\begin{array}{l}x+y= m+1①,\\ x-y= 3m-1②\end{array} \right.的解满足x＞2y$,求$m$的最小整数值.

答案： 由 ① + ② 得 $ x = 2m $，由 ① - ② 得 $ y = -m + 1 $. $ \because x ＞ 2y $，$ \therefore 2m ＞ 2(-m + 1) $，解得 $ m ＞ \frac{1}{2} $. $ \therefore m $ 的最小整数值为 1.