《2025年通城学典课时作业本九年级数学上册苏科版江苏专版》

1. 圆是轴对称图形，过圆心的任意一条直线都是它的对称轴.

答案： 1. 过圆心的任意一条直线

2. 垂径定理:垂直于弦的直径平分弦以及弦所对的两条弧.

答案： 2. 弦 两条弧

1. 如图，$AB$是$\odot O$的弦，直径$MN\bot AB$，垂足为$C$，则下列结论不一定成立的是 (D)

A.$AC=BC$
B.$\overset{\frown}{AN}=\overset{\frown}{BN}$
C.$\overset{\frown}{AM}=\overset{\frown}{BM}$
D.$OC=CN$

答案： 1.D

2. 已知$\odot O$的半径为$7$，$AB$是$\odot O$的弦，点$P$在弦$AB$上. 若$PA=4$，$PB=6$，则$OP$的长为
(D)

A.$\sqrt{14}$
B.$4$
C.$\sqrt{23}$
D.$5$

答案： 2.D

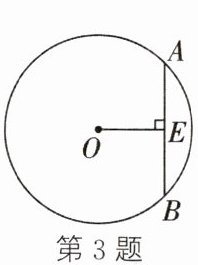
3. (2024·长沙)如图，在$\odot O$中，弦$AB$的长为$8$，圆心$O$到$AB$的距离$OE=4$，则$\odot O$的半径为$4\sqrt{2}$.

答案： $3.4\sqrt{2}$

4. (新情境·现实生活)(2023·永州)如图，$\odot O$是一个盛有水的容器的横截面，$\odot O$的半径为$10\ cm$，水的最深处到水面$AB$的距离为$4\ \text{cm$，则水面$AB$的宽度为16$ cm$.

答案： 4.16

5. （2024·遂宁改编）如图，$AB$是$\odot O$的直径，$AC$是$\odot O$的弦，$D$是$\overset{\frown}{AC}$的中点，$DE\bot AB$于点$E$，交$AC$于点$F$，交$\odot O$于点$H$，$DB$交$AC$于点$G$，连接$AD$.
（1）求证：$AF=DF$；
（2）若$AF=\frac{5}{2} $，$\frac{AE}{AD}=\frac{\sqrt{5}}{5} $，求$AE$的长.

答案： 5.（1）
∵ D 是$\overset{\frown}{AC}$的中点,
∴$\overset{\frown}{AD}=\overset{\frown}{CD}. $
∵AB⊥DH,且 AB是⊙O的直径,
∴$\overset{\frown}{AD}=\overset{\frown}{AH}, $
∴$\overset{\frown}{CD}=\overset{\frown}{AH}, $
∴∠ADH =∠CAD,
∴AF = DF （2）设$AE =\sqrt{5}x,$则AD = 5x.
∵DE⊥AB,
∴∠AED = 90°,
∴在Rt△AED中$,DE =\sqrt{AD^{2}-AE^{2}}= 2\sqrt{5}x. $
∵$AF =\frac{5}{2},AF = DF, $
∴$DF =\frac{5}{2}. $
∵在Rt△AEF中，
$AE^{2}+EF^{2}=AF^{2}, $
∴$(\sqrt{5}x)^{2}+(2\sqrt{5}x-\frac{5}{2})^{2}=(\frac{5}{2})^{2},$解得
$x =\frac{2\sqrt{5}}{5}(x = 0$舍去),
∴$AE =\sqrt{5}x = 2$