1. 在平面内把线段$OP$绕着端点$O$旋转
1周
,端点P
运动所形成的图形叫做圆.其中,点$O$叫做圆心
,线段OP
叫做半径
.
答案:
1. 1周 P 圆心 OP 半径
2. 如果$\odot O$的半径为$r$,点$P$到圆心$O$的距离为$d$,那么(1)点$P$在圆上$\Leftrightarrow d$
(2)点$P$在圆
=
$r$;(2)点$P$在圆
外
$\Leftrightarrow d>r$;(3)点$P$在圆内
$\Leftrightarrow d<r$.
答案:
2.
(1)=
(2)外
(3)内
(1)=
(2)外
(3)内
1. 下列条件中,能确定圆的是 (
A.以已知点$O$为圆心
B.以已知点$O$为圆心,$2\ cm$为半径
C.以$2\ cm$为半径
D.经过已知点$A$,且半径为$2\ cm$
B
)A.以已知点$O$为圆心
B.以已知点$O$为圆心,$2\ cm$为半径
C.以$2\ cm$为半径
D.经过已知点$A$,且半径为$2\ cm$
答案:
1. B
2. 若$\odot O$的直径为$10\ cm$,点$A$到圆心$O$的距离$OA = 6\ cm$,则点$A$与$\odot O$的位置关系为 (
A.点$A$在$\odot O$上
B.点$A$在$\odot O$内
C.点$A$在$\odot O$外
D.无法确定
C
)A.点$A$在$\odot O$上
B.点$A$在$\odot O$内
C.点$A$在$\odot O$外
D.无法确定
答案:
2. C
3. 与点$P$的距离为$12\ cm$的点所组成的平面图形是
以点P为圆心、12cm为半径的圆
.
答案:
3. 以点P为圆心、12cm为半径的圆
4. 如图,在${Rt}\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle A = 30^{\circ}$,$AB = 2\ cm$,以点$A$为圆心画圆.若$\odot A$的半径为$1.8\ cm$,则点$C$在$\odot A$
内
,点$B$在$\odot A$外
.
答案:
4. 内 外
5. (数形结合思想)已知$\odot N$的半径为$3$,点$M$与点$N$之间的距离为$d$,且关于$x$的方程$x^{2} - 2\sqrt{3}x + d = 0$有两个相等的实数根,则点$M$与$\odot N$的位置关系是
点M在⊙N上
.
答案:
5. 点M在⊙N上
6. 如图,在四边形$ABCD$中,$\angle ABC = \angle ADC = 90^{\circ}$.求证:点$A$、$B$、$C$、$D$在同一个圆上.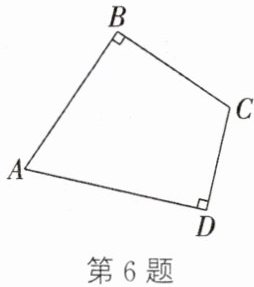

答案:
6. 如图,连接AC,取AC的中点O,连接OB、OD.
∵∠ABC=90°,O是AC的中点,
∴OB=OA=OC.同理,可证OD=OA,
∴OB=OA=OC=OD,
∴点A、B、C、D在同一个圆上

6. 如图,连接AC,取AC的中点O,连接OB、OD.
∵∠ABC=90°,O是AC的中点,
∴OB=OA=OC.同理,可证OD=OA,
∴OB=OA=OC=OD,
∴点A、B、C、D在同一个圆上

查看更多完整答案,请扫码查看


