《2025年高考领航高中同步测试卷高中数学必修第二册人教版》

7.如图，由四个全等的直角三角形与一个小正方形拼成的一个大正方形中，$\overrightarrow{AB}=\boldsymbol{a}$，$\overrightarrow{AD}=\boldsymbol{b}$，$\overrightarrow{AF}=2\overrightarrow{FE}$，则$\overrightarrow{AE}=$ ( )

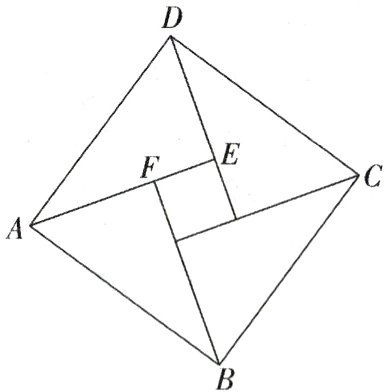
A.$\frac{3}{4}\boldsymbol{a}+\frac{1}{2}\boldsymbol{b}$
B.$\frac{12}{25}\boldsymbol{a}+\frac{16}{25}\boldsymbol{b}$
C.$\frac{6}{13}\boldsymbol{a}+\frac{9}{13}\boldsymbol{b}$
D.$\frac{2}{7}\boldsymbol{a}+\frac{3}{7}\boldsymbol{b}$

答案： $\because\overrightarrow{AF}=2\overrightarrow{FE}$，$\therefore\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AD}+\frac{2}{3}\overrightarrow{FB}=\overrightarrow{AD}+\frac{2}{3}(\overrightarrow{AB}-\overrightarrow{AF})=\overrightarrow{AD}+\frac{2}{3}(\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AE})=\overrightarrow{AD}+\frac{2}{3}\overrightarrow{AB}-\frac{4}{9}\overrightarrow{AE}$，$\therefore\frac{13}{9}\overrightarrow{AE}=\frac{2}{3}\overrightarrow{AB}+\overrightarrow{AD}$，$\therefore\overrightarrow{AE}=\frac{6}{13}\boldsymbol{a}+\frac{9}{13}\boldsymbol{b}$.

8.放风筝是一项集书画艺术、制作技艺、健身娱乐、竞技比赛于一体的文化体育活动，具有悠久的历史和鲜明的地方特色.风筝是中华民族文化宝库中的一颗“明珠”.现有一个风筝骨架如图所示，已知$O$为正方形$ABCD$的对角线交点，等边三角形$ACP$的边长为2，则$\overrightarrow{PO}\cdot\overrightarrow{AB}=$( )

A.$\sqrt{3}$
B.$\sqrt{2}$
C.1
D.$\frac{1}{2}$

答案： 设$\theta=\langle\overrightarrow{PO},\overrightarrow{AB}\rangle$，易知$\theta = 45^{\circ}$，因为等边三角形$ACP$的边长为$2$，易知$PO$是$\triangle ACP$的高，所以$PO=\frac{\sqrt{3}}{2}\times2=\sqrt{3}$，即$\vert\overrightarrow{PO}\vert=\sqrt{3}$，正方形的边长为$\frac{AC}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}$，即$\vert\overrightarrow{AB}\vert=\sqrt{2}$，所以$\overrightarrow{PO}\cdot\overrightarrow{AB}=\sqrt{3}\times\sqrt{2}\times\cos45^{\circ}=\sqrt{3}$.

9.对于任意两个向量$\boldsymbol{a}$和$\boldsymbol{b}$，下列命题为真命题的是 ( )
A.若$\boldsymbol{a}$，$\boldsymbol{b}$满足$\vert\boldsymbol{a}\vert ＞ \vert\boldsymbol{b}\vert$，且$\boldsymbol{a}$与$\boldsymbol{b}$同向，则$\boldsymbol{a} ＞ \boldsymbol{b}$
B.$\vert\boldsymbol{a}+\boldsymbol{b}\vert\leqslant\vert\boldsymbol{a}\vert + \vert\boldsymbol{b}\vert$
C.$\vert\boldsymbol{a}\cdot\boldsymbol{b}\vert\leqslant\vert\boldsymbol{a}\vert\vert\boldsymbol{b}\vert$
D.$\vert\boldsymbol{a}-\boldsymbol{b}\vert\leqslant\vert\boldsymbol{a}\vert - \vert\boldsymbol{b}\vert$

答案： A项错误，向量不能比较大小；
B项正确，利用向量的加法运算法则可判断；
C项正确，设$\boldsymbol{a}$与$\boldsymbol{b}$的夹角为$\theta$，则$\vert\boldsymbol{a}\cdot\boldsymbol{b}\vert=\vert\boldsymbol{a}\vert\cdot\vert\boldsymbol{b}\vert\cdot\cos\theta\leq\vert\boldsymbol{a}\vert\vert\boldsymbol{b}\vert$；
D项错误，$\vert\boldsymbol{a}-\boldsymbol{b}\vert\geq\vert\vert\boldsymbol{a}\vert-\vert\boldsymbol{b}\vert\vert$.
故选BC.

10.在$\triangle ABC$中，下列命题正确的有 ( )
A.$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$
B.$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\boldsymbol{0}$
C.点$O$为$\triangle ABC$的内心，且$(\overrightarrow{OB}-\overrightarrow{OC})\cdot(\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA}) = 0$，则$\triangle ABC$为等腰三角形
D.$\overrightarrow{AC}\cdot\overrightarrow{AB} ＞ 0$，则$\triangle ABC$为锐角三角形

答案： A.$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$，故A错误；
B.$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\boldsymbol{0}$，故B正确；C. 点$O$为$\triangle ABC$的内心，且$(\overrightarrow{OB}-\overrightarrow{OC})\cdot(\overrightarrow{OB}+\overrightarrow{OC}-2\overrightarrow{OA})=0$，则$AB = AC$，所以$\triangle ABC$为等腰三角形，故C正确；D.$\overrightarrow{AC}\cdot\overrightarrow{AB}＞0$，则$\angle BAC$是锐角，但$\triangle ABC$不一定为锐角三角形，故D错误. 故选BC.

11.如图，已知半圆$O$上有一个动点$C$，$F$是$AC$上靠近点$C$的三等分点，且$OC$与$BF$交于点$E$，则下列结论正确的有 ( )

A.$\overrightarrow{AE}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}$
B.$\overrightarrow{CE}=\frac{1}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$
C.$\overrightarrow{BF}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$
D.$\overrightarrow{EF}=-\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$

答案： 如图，对于A选项，取$AF$的中点$H$，连接$OH$.
因为$O$是$AB$的中点，所以在$\triangle ABF$中，$OH// BF$，所以$OH// EF$.
因为$F$是靠近点$C$的三等分点，所以$F$是$HC$的中点，从而$E$是$CO$的中点，所以$\overrightarrow{AE}=\frac{1}{2}(\overrightarrow{AC}+\overrightarrow{AO})=\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{AB}$，A正确；
对于B选项，$\overrightarrow{CE}=\frac{1}{2}\overrightarrow{CO}=\frac{1}{2}(\overrightarrow{AO}-\overrightarrow{AC})=\frac{1}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}$，B正确；
对于C选项，$\overrightarrow{BF}=\overrightarrow{AF}-\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AC}-\overrightarrow{AB}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{BC})-\overrightarrow{AB}=-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$，C错误；
对于D选项，$\overrightarrow{EF}=\overrightarrow{AF}-\overrightarrow{AE}=\frac{2}{3}\overrightarrow{AC}-(\frac{1}{2}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{AB})=\frac{1}{6}\overrightarrow{AC}-\frac{1}{4}\overrightarrow{AB}$，D正确. 故选ABD.