2025年周末小复习四年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年周末小复习四年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
2. 我的叔叔是一名风筝爱好者,经过多次实践,叔叔终于成功制作出了一只板鹞风筝(如右图,板鹞风筝的主体是由一个正方形和一个长方形组成)。
我的叔叔是一名风筝爱好者,经过多次实践,叔叔终于成功制作出了一只板鹞风筝(如右图,板鹞风筝的主体是由一个正方形和一个长方形组成)。

(1)为节约材料,小维想利用叔叔之前制作的正方形风筝骨架改造成三角形造型的风筝(如图)。假如这个风筝骨架是一个等边三角形,那么边长应该是多少分米? (6分)
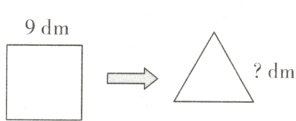
(2)假如风筝骨架是一个等腰三角形,其中一条边是10 dm,另外两条边的长是多少? (请写出所有的可能)(6分)
 我的叔叔是一名风筝爱好者,经过多次实践,叔叔终于成功制作出了一只板鹞风筝(如右图,板鹞风筝的主体是由一个正方形和一个长方形组成)。
我的叔叔是一名风筝爱好者,经过多次实践,叔叔终于成功制作出了一只板鹞风筝(如右图,板鹞风筝的主体是由一个正方形和一个长方形组成)。 
(1)为节约材料,小维想利用叔叔之前制作的正方形风筝骨架改造成三角形造型的风筝(如图)。假如这个风筝骨架是一个等边三角形,那么边长应该是多少分米? (6分)

(2)假如风筝骨架是一个等腰三角形,其中一条边是10 dm,另外两条边的长是多少? (请写出所有的可能)(6分)
答案:
(1) 9×4 = 36(dm) 36÷3 = 12(dm)
答:那么边长应该是12 dm。
(2) 等腰三角形其中一条边是10 dm,如果这个边是等腰的边,36 - 10 - 10 = 16(dm),那么另外两条边的长是10 dm,16 dm。如果这个边不是等腰的边,(36 - 10)÷2 = 13(dm),那么另外两条边的长是13 dm,13 dm。
答:另外两边的长是10 dm,16 dm或13 dm,13 dm。
(1) 9×4 = 36(dm) 36÷3 = 12(dm)
答:那么边长应该是12 dm。
(2) 等腰三角形其中一条边是10 dm,如果这个边是等腰的边,36 - 10 - 10 = 16(dm),那么另外两条边的长是10 dm,16 dm。如果这个边不是等腰的边,(36 - 10)÷2 = 13(dm),那么另外两条边的长是13 dm,13 dm。
答:另外两边的长是10 dm,16 dm或13 dm,13 dm。
3. 聪聪折纸花时先将一张正方形对折,展开得到一条折痕,然后将正方形纸的左上和右上两个角的顶点折到折痕上的点A处,试判断∠1与∠2的大小关系。(10分)


答案:
根据题图可知,三角形ABC三边相等,是等边三角形。如图,∠3 = ∠4 = 60°,根据折叠的性质和三角形内角和可得,∠5 = (90° - 60°)÷2 = 15°,∠6 = 180° - 90° - 15° = 75°,∠1 = 180° - 75°×2 = 30°;∠7 = (90° - 60°)÷2 = 15°,∠8 = 180° - 90° - 15° = 75°,∠2 = 180° - 75°×2 = 30°,所以∠1 = ∠2。

根据题图可知,三角形ABC三边相等,是等边三角形。如图,∠3 = ∠4 = 60°,根据折叠的性质和三角形内角和可得,∠5 = (90° - 60°)÷2 = 15°,∠6 = 180° - 90° - 15° = 75°,∠1 = 180° - 75°×2 = 30°;∠7 = (90° - 60°)÷2 = 15°,∠8 = 180° - 90° - 15° = 75°,∠2 = 180° - 75°×2 = 30°,所以∠1 = ∠2。

(新考法)三角形的一条边与另一条边的延长线组成的角叫做三角形的外角。下图三角形中,∠1、∠2、∠3是三角形的三个内角,∠4、∠5、∠6是它的三个外角。
1. 请你根据三角形内角和计算推导出三角形外角和。

2. 请计算出四边形、五边形的外角和,你发现多边形的外角和有什么规律吗?
1. 请你根据三角形内角和计算推导出三角形外角和。

2. 请计算出四边形、五边形的外角和,你发现多边形的外角和有什么规律吗?
答案:
1. ∠1 + ∠2 + ∠3 = 180°,∠4 = 180° - ∠1,∠5 = 180° - ∠2,∠6 = 180° - ∠3,
三角形外角和:∠4 + ∠5 + ∠6 = 180° - ∠1 + 180° - ∠2 + 180° - ∠3 = 180° + 180° + 180° - (∠1 + ∠2 + ∠3) = 540° - 180° = 360°。
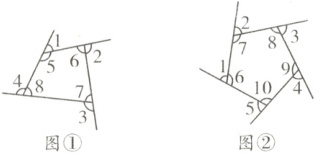
2. 如图①,∠1 = 180° - ∠5,∠2 = 180° - ∠6,∠3 = 180° - ∠7,∠4 = 180° - ∠8,∠5 + ∠6 + ∠7 + ∠8 = 360°,四边形外角和:∠1 + ∠2 + ∠3 + ∠4 = 180° - ∠5 + 180° - ∠6 + 180° - ∠7 + 180° - ∠8 = 180°×4 - (∠5 + ∠6 + ∠7 + ∠8) = 720° - 360° = 360°。
如图②,∠1 = 180° - ∠6,∠2 = 180° - ∠7,∠3 = 180° - ∠8,∠4 = 180° - ∠9,∠5 = 180° - ∠10,∠6 + ∠7 + ∠8 + ∠9 + ∠10 = 180°×(5 - 2) = 540°,五边形外角和:∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 180° - ∠6 + 180° - ∠7 + 180° - ∠8 + 180° - ∠9 + 180° - ∠10 = 180°×5 - (∠6 + ∠7 + ∠8 + ∠9 + ∠10) = 900° - 540° = 360°。
我发现多边形的外角和均为360°。
1. ∠1 + ∠2 + ∠3 = 180°,∠4 = 180° - ∠1,∠5 = 180° - ∠2,∠6 = 180° - ∠3,
三角形外角和:∠4 + ∠5 + ∠6 = 180° - ∠1 + 180° - ∠2 + 180° - ∠3 = 180° + 180° + 180° - (∠1 + ∠2 + ∠3) = 540° - 180° = 360°。
2. 如图①,∠1 = 180° - ∠5,∠2 = 180° - ∠6,∠3 = 180° - ∠7,∠4 = 180° - ∠8,∠5 + ∠6 + ∠7 + ∠8 = 360°,四边形外角和:∠1 + ∠2 + ∠3 + ∠4 = 180° - ∠5 + 180° - ∠6 + 180° - ∠7 + 180° - ∠8 = 180°×4 - (∠5 + ∠6 + ∠7 + ∠8) = 720° - 360° = 360°。
如图②,∠1 = 180° - ∠6,∠2 = 180° - ∠7,∠3 = 180° - ∠8,∠4 = 180° - ∠9,∠5 = 180° - ∠10,∠6 + ∠7 + ∠8 + ∠9 + ∠10 = 180°×(5 - 2) = 540°,五边形外角和:∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 180° - ∠6 + 180° - ∠7 + 180° - ∠8 + 180° - ∠9 + 180° - ∠10 = 180°×5 - (∠6 + ∠7 + ∠8 + ∠9 + ∠10) = 900° - 540° = 360°。
我发现多边形的外角和均为360°。

查看更多完整答案,请扫码查看


