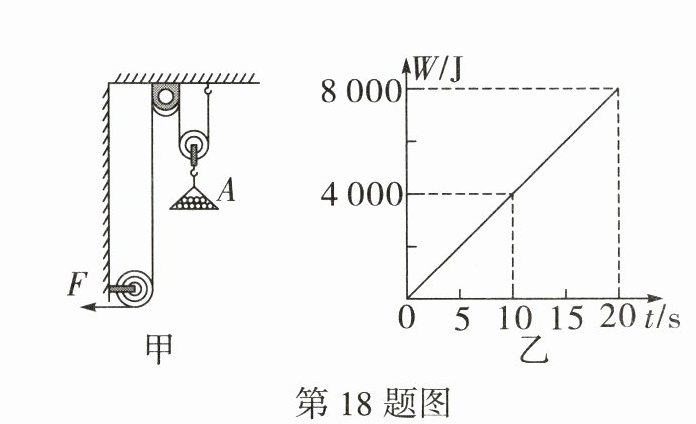
18. 如图甲所示是建筑工地上使用的小型“罐笼式”提升机,它能将不易捆绑的建筑材料放入罐笼A中提升到高处,某次在不使用罐笼的情况下,在拉力F的作用下,将重为500 N的重物以0.5 m/s的速度匀速提升. 拉力F做的功W随时间t的变化图像如图乙所示.(不计绳重和滑轮与轴之间的摩擦,g取10 N/kg)求:
(1)将重物提升2.5 m,滑轮组做的有用功.
(2)将重物提升2.5 m,此过程中滑轮组的机械效率.
(3)若绳子能承受的最大拉力是2 000 N,罐笼A重为1 200 N,提升机始终不离开地面,求使用罐笼A时,提升机可提升物体的最大重力.
(1)将重物提升2.5 m,滑轮组做的有用功.
(2)将重物提升2.5 m,此过程中滑轮组的机械效率.
(3)若绳子能承受的最大拉力是2 000 N,罐笼A重为1 200 N,提升机始终不离开地面,求使用罐笼A时,提升机可提升物体的最大重力.

答案:
解:
(1)滑轮组做的有用功$W_{有}=G_{物}h = 500\ N×2.5\ m = 1250\ J$……(2分)
(2)利用同样的滑轮组匀速提升同一物体的过程中机械效率不变。重物提升2.5 m所用时间$t=\frac{h}{v}=\frac{2.5\ m}{0.5\ m/s}=5\ s$……(2分) 由题图乙可知5 s内拉力做的总功$W_{总}=2000\ J$……(1分) 滑轮组的机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{1250\ J}{2000\ J}×100\% = 62.5\%$……(2分)
(3)由题图甲可知承担物重的绳子段数为2 由$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{G_{物}}{G_{物}+G_{动}}×100\%$得动滑轮的重力$G_{动}=\frac{G_{物}}{\eta}-G_{物}=\frac{500\ N}{62.5\%}-500\ N = 300\ N$……(2分) 由$F_{拉}=\frac{1}{2}(G_{物}'+G_{动}+G_{A})$可得绳子能承受的最大拉力$F_{拉max}=\frac{1}{2}(G_{物max}+G_{动}+G_{A})$……(2分) 提升机可提升物体的最大重力$G_{物max}=2F_{拉max}-G_{动}-G_{A}=2×2000\ N - 300\ N - 1200\ N = 2500\ N$……(2分)
(1)滑轮组做的有用功$W_{有}=G_{物}h = 500\ N×2.5\ m = 1250\ J$……(2分)
(2)利用同样的滑轮组匀速提升同一物体的过程中机械效率不变。重物提升2.5 m所用时间$t=\frac{h}{v}=\frac{2.5\ m}{0.5\ m/s}=5\ s$……(2分) 由题图乙可知5 s内拉力做的总功$W_{总}=2000\ J$……(1分) 滑轮组的机械效率$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{1250\ J}{2000\ J}×100\% = 62.5\%$……(2分)
(3)由题图甲可知承担物重的绳子段数为2 由$\eta=\frac{W_{有}}{W_{总}}×100\%=\frac{G_{物}}{G_{物}+G_{动}}×100\%$得动滑轮的重力$G_{动}=\frac{G_{物}}{\eta}-G_{物}=\frac{500\ N}{62.5\%}-500\ N = 300\ N$……(2分) 由$F_{拉}=\frac{1}{2}(G_{物}'+G_{动}+G_{A})$可得绳子能承受的最大拉力$F_{拉max}=\frac{1}{2}(G_{物max}+G_{动}+G_{A})$……(2分) 提升机可提升物体的最大重力$G_{物max}=2F_{拉max}-G_{动}-G_{A}=2×2000\ N - 300\ N - 1200\ N = 2500\ N$……(2分)
查看更多完整答案,请扫码查看


