第12页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
5. 为了让学生体验劳动的艰辛与乐趣,某学校组织四年级学生开展掰玉米劳动教育实践活动,其中一块玉米地如图所示。(8分)
(1)这块玉米地的面积是多少平方米?(4分)
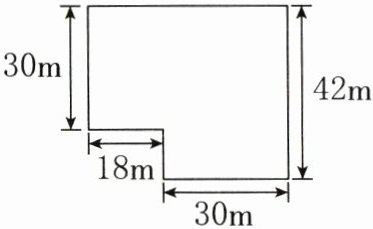
(2)四年级学生被分成15个小组,每个小组有6名学生,共掰了810个玉米,平均每名学生掰多少个玉米?(4分)
(1)这块玉米地的面积是多少平方米?(4分)

(2)四年级学生被分成15个小组,每个小组有6名学生,共掰了810个玉米,平均每名学生掰多少个玉米?(4分)
答案:
(1)30×18+30×42 = 1800(m²)
(2)810÷(15×6) = 9(个)
(1)30×18+30×42 = 1800(m²)
(2)810÷(15×6) = 9(个)
1. 在$\square$里填上合适的数。(6分)
$245×5 + 245×4 + 245×1 = 245×\square$
$156×125 - 50×125 - 6×125 = \square×125$
$167×34 + 167×67 - 167 = \square×\square$
$245×5 + 245×4 + 245×1 = 245×\square$
$156×125 - 50×125 - 6×125 = \square×125$
$167×34 + 167×67 - 167 = \square×\square$
答案:
10 100 167 100 解析:逆用乘法分配律可得,$245×5 + 245×4 + 245×1 = 245×(5 + 4 + 1) = 245×10$;$156×125 - 50×125 - 6×125 = 125×(156 - 50 - 6) = 125×100$;$167×34 + 167×67 - 167 = 167×(34 + 67 - 1) = 167×100$。
2. 淘淘由于粗心大意把$60×(\square + 6)$错算成了$60×\square + 6$,他得到的结果与正确结果相差( )。
(4分)
A. 360
B. 36
C. 366
D. 354
(4分)
A. 360
B. 36
C. 366
D. 354
答案:
D 解析:原算式利用乘法分配律去括号为$60×(□ + 6) = 60×□ + 60×6 = 60×□ + 360$,淘淘由于粗心大意把$60×(□ + 6)$错算成了$60×□ + 6$,也就是把$60×□ + 360$错算成了$60×□ + 6$,所以他得到的结果与正确结果相差$360 - 6 = 354$。
3. 用合适的方法计算。(10分)
(1)$1 + 3 + 5 + 7 + \cdots + 95 + 97 + 99$ (2)$222×999 + 333×334$
(1)$1 + 3 + 5 + 7 + \cdots + 95 + 97 + 99$ (2)$222×999 + 333×334$
答案:
(1)$1 + 3 + 5 + 7 + \cdots + 95 + 97 + 99$
$=(1 + 99)+(3 + 97)+(5 + 95)+\cdots+(49 + 51)$
$=100×50÷2$
$=5000÷2$
$=2500$
解析:观察算式,发现第一个数和最后一个数可以凑成 100,第二个数和倒数第二个数可以凑成 100,第三个数和倒数第三个数可以凑成 100……第 25 个数和倒数第 25 个数可以凑成 100,刚好凑成 25 个 100,所以结果是 2500。
(2)$222×999 + 333×334$
$=222×333×3 + 333×334$
$=333×222×3 + 333×334$
$=333×(222×3 + 334)$
$=333×(666 + 334)$
$=333×1000$
$=333000$
解析:看到 999 和 333 我们就会想到$999 = 333×3$,所以$222×999 = 222×333×3$,所以$222×999 + 333×334 = 222×333×3 + 333×334 = 333×222×3 + 333×334 = 333×(222×3 + 334) = 333×(666 + 334) = 333×1000 = 333000$。
$=(1 + 99)+(3 + 97)+(5 + 95)+\cdots+(49 + 51)$
$=100×50÷2$
$=5000÷2$
$=2500$
解析:观察算式,发现第一个数和最后一个数可以凑成 100,第二个数和倒数第二个数可以凑成 100,第三个数和倒数第三个数可以凑成 100……第 25 个数和倒数第 25 个数可以凑成 100,刚好凑成 25 个 100,所以结果是 2500。
(2)$222×999 + 333×334$
$=222×333×3 + 333×334$
$=333×222×3 + 333×334$
$=333×(222×3 + 334)$
$=333×(666 + 334)$
$=333×1000$
$=333000$
解析:看到 999 和 333 我们就会想到$999 = 333×3$,所以$222×999 = 222×333×3$,所以$222×999 + 333×334 = 222×333×3 + 333×334 = 333×222×3 + 333×334 = 333×(222×3 + 334) = 333×(666 + 334) = 333×1000 = 333000$。
查看更多完整答案,请扫码查看


