《2025年黄冈小状元作业本四年级数学下册北师大版广东专版》

1. 探究题 下面是三位同学探究“三角形内角和”的方法。

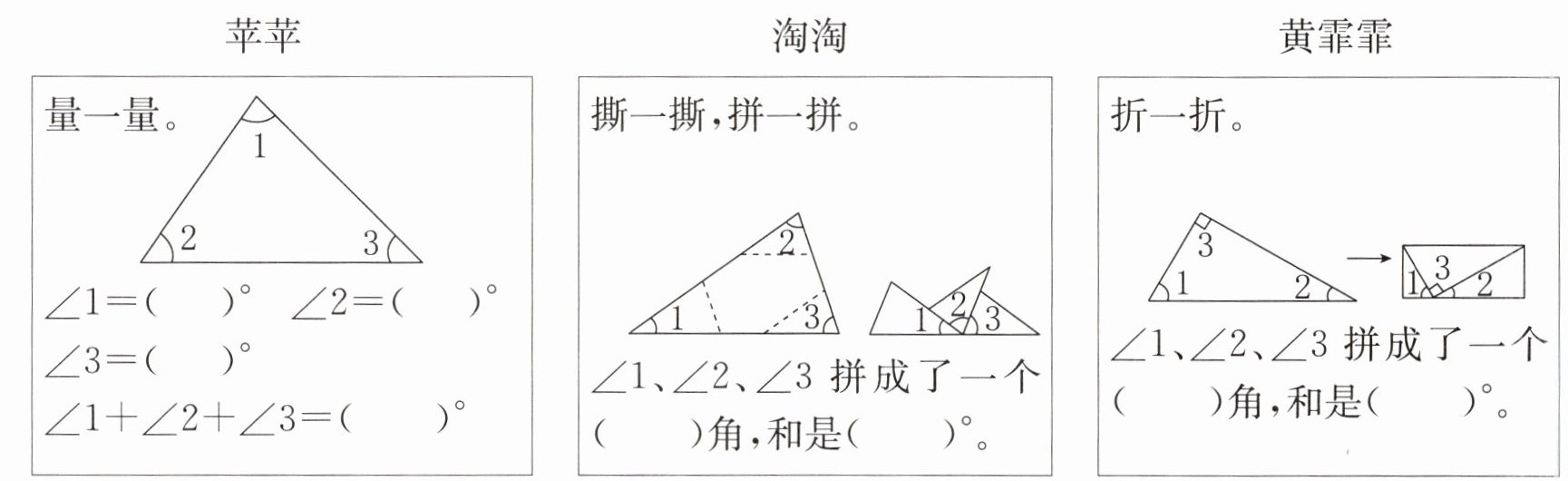
探究发现:三角形的内角和是(　　　　)°

答案： 80 55 45 180；平 180；平 180；180

2. 选一选。(将正确答案的序号填在括号里)
(1) 一个三角形中有一个直角和一个锐角,那么第三个内角一定是(　　　)。
A. 锐角　　　　　　　B. 直角　　　　　　　C. 钝角　　　　　　　D. 无法确定
(2) 易错题 一个钝角三角形,它的两个锐角的和(　　　)90°
A. 大于　　　　　　　B. 等于　　　　　　　C. 小于　　　　　　　D. 无法确定

答案：
(1)A
(2)C

3. 用两把完全相同的三角尺 分别拼成一个三角形和一个四边形。
(1) 
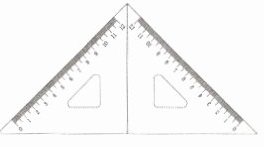
这个三角形的内角和是(　　　)°。
(2)
这个四边形的内角和是(　　　)°。

答案：
(1)180
(2)360
解析：两把三角尺都是等腰直角三角形，都有一个90°的顶角和两个45°的底角。
(1)拼成的三角形的内角和就是4个45°角的度数之和，即45°+45°+45°+45°=180°。
(2)拼成的四边形的内角和就是4个45°角和2个90°角的度数之和，即45°+45°+45°+45°+90°+90°=360°。

4. 填表。(根据三角形内角和等于180°,试求下表中其他图形的内角和)

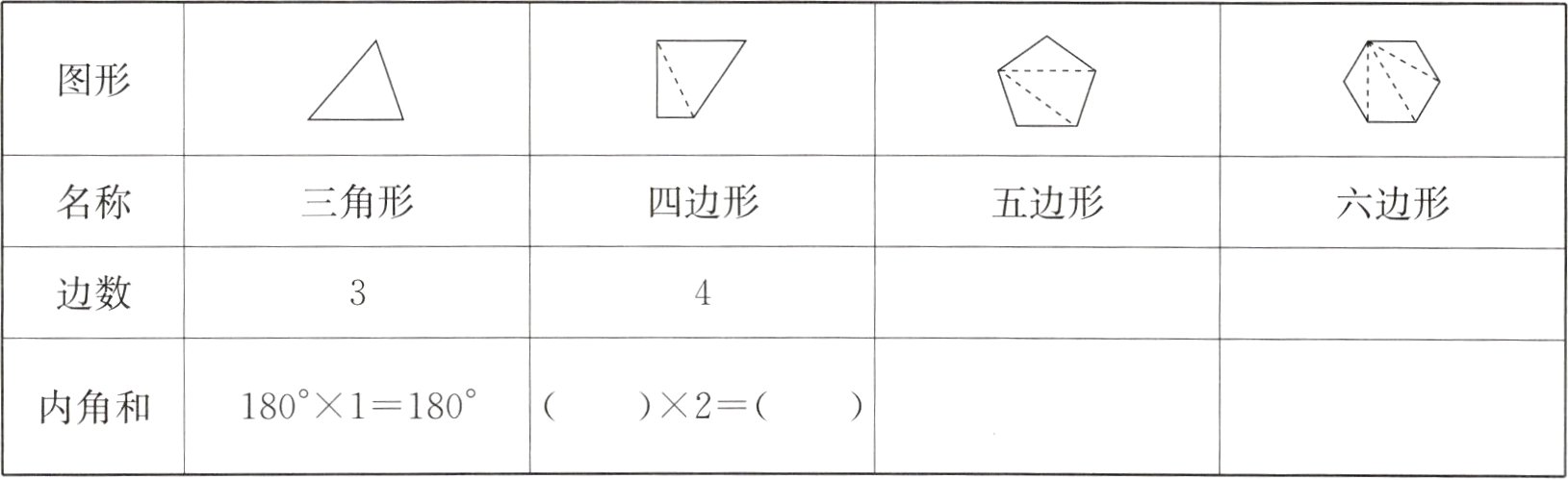
答案： (按列填)180° 360°；5 180°×3=540°；6 180°×4=720°
解析：本题可利用转换的思想求解，可以将各多边形拆分成多个三角形，根据“三角形内角和等于180°”，能分成几个三角形，就用180°乘几，就能求出各多边形的内角和。最后发现多边形的内角和=180°×(多边形的边数 - 2)。

 5.1 - 0.08 =  4.3 - 0.35 =  15.4 - 4.6 =  7.6 + 2.4 =  4.04 + 3.6 =

答案：