《2024年学评手册六年级数学上册北师大版》

1. 我们通过测量圆的直径和周长,发现圆的周长总是其直径的( )倍多一些,这也是古人最早使用的方法。魏晋时期杰出的数学家刘徽用( )较精确地得到圆周率的近似值是( )。

答案： 3
割圆术
3.14

2. 1500多年前,我国南北朝时期著名的数学家祖冲之算出π的值在( )和( )之间。

答案： 3.1415926
3.1415927

3. 圆周率π是一个无限( )小数。

答案： 不循环

4.

照这样画下去,最后一个图形越来越接近( )。

答案： 圆

5.

照这样画下去,内接正多边形的周长越来越接近( )。

照这样画下去,外切正多边形的周长越来越接近( )。
对照以上过程,你得出结论：( )。

答案：
圆的周长
圆的周长
正多边形的边数越多，越接近圆

6. 先量一量,再按要求画一画、算一算
(1) 在正方形里面画一个最大的圆,然后算出这个圆的周长。

(2) 在正方形外面画一个圆,使正方形的四个顶点都在圆上,然后算出这个圆的周长。

答案：


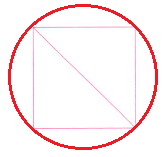
3.14×3=9.42(cm)
3.14×2=6.28(cm)

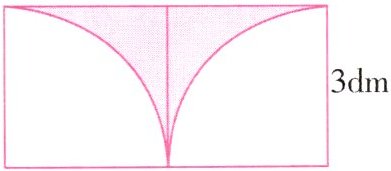
7. 计算右图中阴影部分的周长

答案： 3.14×2×3÷2+3×2=15.42(dm)
答：阴影部分的周长是15.42分米。