知识迁移 (教材 P2 例题变式题)下图中,点 O 是圆的(
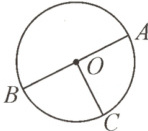
圆心
),线段 OC 是圆的(半径
),通常用字母(r
)表示,线段 AB 是圆的(直径
),通常用字母(d
)表示。如果 OC = 3 cm,那么 AB = (6
)cm。
答案:
知识迁移 圆心 半径 r 直径 d 6
(1) 在同一个圆里,可以画(
无数
)条半径,(无数
)条直径,所有的半径都(相等
),所有的直径都(相等
)。
答案:
1.
(1)无数 无数 相等 相等
(1)无数 无数 相等 相等
(2) 把圆规的两脚分开,使两脚间的距离是 6 cm,那么画出的圆的半径是(
6
)cm,直径是(12
)cm。
答案:
1.
(2)6 12
(2)6 12
(3) 如图,小朋友们玩套圈游戏时,他们自动围成了圆形,这是因为(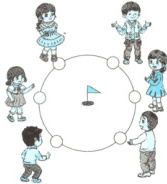
所有小朋友与小旗之间的距离都相等
)。
答案:
1.
(3)所有小朋友与小旗之间的距离都相等
(3)所有小朋友与小旗之间的距离都相等
2. (易错)判断。(对的画“√”,错的画“×”)
(1) 直径是圆内最长的线段。 (
(2) 在同一个圆中,两条半径就是一条直径。 (
(3) 一个圆心只能画一个圆。 (
(1) 直径是圆内最长的线段。 (
√
)(2) 在同一个圆中,两条半径就是一条直径。 (
×
)(3) 一个圆心只能画一个圆。 (
×
)
答案:
2.
(1)√
(2)×
(3)×
(1)√
(2)×
(3)×
3. 填表。


答案:
3.10 cm 1.5 cm 0.4 dm 0.75 m
(1) 画一个直径是 2 cm 的圆,并用字母 O,r,d 标出它的圆心、半径和直径。
答案:
(1)
画图步骤:用圆规两脚间距离定为$2÷2 = 1cm$,固定针尖在纸上画圆;在圆中心标$O$,从$O$到圆上取一点连线标$r$,过$O$和圆上两点(在同一直线)连线标$d$。
(1)
画图步骤:用圆规两脚间距离定为$2÷2 = 1cm$,固定针尖在纸上画圆;在圆中心标$O$,从$O$到圆上取一点连线标$r$,过$O$和圆上两点(在同一直线)连线标$d$。
(2) 以点 O 为圆心,画两个半径不相等的圆,并画出每个圆的一条直径。
答案:
(2)
画图步骤:先定点$O$,用圆规以不同半径(如$1.5cm$和$2.5cm$)绕$O$画两个圆;在每个圆上过$O$画一条直线与圆相交两点,即为直径。
(2)
画图步骤:先定点$O$,用圆规以不同半径(如$1.5cm$和$2.5cm$)绕$O$画两个圆;在每个圆上过$O$画一条直线与圆相交两点,即为直径。
5. (生活运用)体育课上,老师想在操场上画一个半径是 7 m 的大圆做游戏,但没有这么大的圆规。请你帮体育老师想想办法,画出这个大圆,并写下来。
答案:
5.示例:在两根木棍中间拴一条长7 m的绳子(接头处忽略不计),一根固定在中心点,拉紧绳子,将另一根木棍绕中心点旋转一周,就能画出这个大圆。(答案不唯一)
6. 已知线段 AB 的长度是 30 cm,大圆的半径和小圆的半径分别是多少厘米?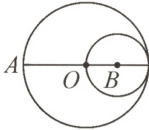

答案:
6.30÷3=10(cm) 10×2=20(cm)
答:大圆的半径是20 cm,小圆的半径是10 cm。
【解析】观察图可知,小圆的直径等于大圆的半径,并且AB的长度等于大圆的半径加上小圆的半径,即3个小圆的半径等于30 cm,从而可以求出大圆和小圆的半径。
答:大圆的半径是20 cm,小圆的半径是10 cm。
【解析】观察图可知,小圆的直径等于大圆的半径,并且AB的长度等于大圆的半径加上小圆的半径,即3个小圆的半径等于30 cm,从而可以求出大圆和小圆的半径。
查看更多完整答案,请扫码查看


