【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);
(2)设(1)中的直线![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.

参考答案:
【答案】(1)作图见解析;(2)证明见解析.
【解析】试题分析:
(1)如图1,用“尺规作图”作出∠ABC的角平分线,再反向延长即可得到![]() ;再用“尺规作图”作出BC的垂直平分线
;再用“尺规作图”作出BC的垂直平分线![]() 即可;
即可;
(2)如图2,连接PB、PC,由题意易证△PBE≌△PCF,从而可得BE=CF.
试题解析:
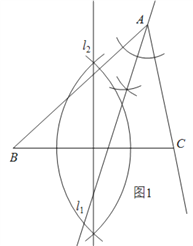
(1)如图1,图中直线![]() 和直线
和直线![]() 为题中所求直线;
为题中所求直线;
(2)如图2,连接PB、PC,
∵AP平分∠BAC,PE⊥AB于点E,PF⊥AC于点F,
∴PE=PF,∠PEB=∠PFC=90°,
∵![]() 垂直平分BC,点P在
垂直平分BC,点P在![]() 上,
上,
∴PB=PC,
∴△PBE≌△PCF,
∴BE=CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:

(1)写出用含x、y的代数式表示厨房的面积是________m2;卧室的面积是________m2;
(2)写出用含x、y的代数式表示这套房的总面积是多少平方米?
(3)当x=3,y=2时,求小王这套房的总面积是多少平方米?
(4)若在(3)中,小王到某商店挑选了80cm×80cm的地砖来镶客厅和卧室,他应买多少块才够用?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x+y=2,xy=-1,则x2+y2=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是等腰三角形,腰上的高为8cm,面积为40cm2,则该三角形的周长是_______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______ cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD是△ABC的中线,若△ABD与△ACD的周长分别是14和12.△ABC的周长是20,则AD的长为 .
相关试题

