【题目】某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.

参考答案:
【答案】(1)见解析;(2)见解析;(3)选择建圆形花坛面积较大
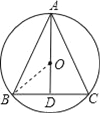
【解析】试题分析:(1)过![]() 作圆即可,具体作法是:分别作
作圆即可,具体作法是:分别作![]() 的垂直平分线,两线交于点
的垂直平分线,两线交于点![]() ,以
,以![]() 为圆心,
为圆心, ![]() 长为半径即可作圆;
长为半径即可作圆;
(2)分别过![]() 作
作![]() 的平行线,两线交于点
的平行线,两线交于点![]() ,平行四边形
,平行四边形![]() 即为所求;
即为所求;
(3)连接![]() 并延长交
并延长交![]() 于
于![]() .可知
.可知![]() 是等边三角形的高,连接
是等边三角形的高,连接![]() ,在
,在![]() 中,利用
中,利用![]() ,结合三角函数,求出半径和圆的面积,而平行四边形的面积等于
,结合三角函数,求出半径和圆的面积,而平行四边形的面积等于![]() 面积的2倍,比较即可求出答案.
面积的2倍,比较即可求出答案.
试题解析:(1)(2)
 ;
;
![]() 连接
连接![]() 延长
延长![]() 交
交![]() 于
于![]() .
.
![]()
![]()
又![]() 平行四边形=
平行四边形=![]()
![]() 平行四边形,
平行四边形,
∴选择建圆形花坛面积较大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC是等腰三角形,腰上的高为8cm,面积为40cm2,则该三角形的周长是_______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线
 和边BC的垂直平分线
和边BC的垂直平分线 (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);(2)设(1)中的直线
 和直线
和直线 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A被这个圆所覆盖.回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是______ cm;
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是______ cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AD是△ABC的中线,若△ABD与△ACD的周长分别是14和12.△ABC的周长是20,则AD的长为 .
-
科目: 来源: 题型:
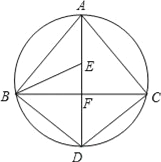
查看答案和解析>>【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

相关试题

