【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
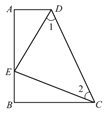
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
参考答案:
【答案】(1)证明见解析; (2)证明见解析.
【解析】试题分析:(1)本题根据已知得出DE=CE,利用HL定理得出两个三角形全等; (2)利用全等三角形的性质得出对应角相等,利用等角的余角相等得出∠DEC=90°即可.
试题解析:
(1)全等.理由是:
∵∠1=∠2,
∴DE=CE
.∵∠A=∠B=90°,AE=BC,
∴Rt△ADE≌Rt△BEC(HL).
(2)是直角三角形.理由是:
∵Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE.
∵∠ECB+∠BEC=90°,
∴∠AED+∠BEC=90°.
∴∠DEC=90°,
∴△CDE是直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形
B.面积相等的三角形
C.直角三角形
D.周长相等的三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:x+y=3,xy=﹣8,求:
(1)x2+y2;
(2)(x2﹣1)(y2﹣1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算x2-2x2的结果是()
A. -1 B. -x4 C. -x2 D. x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
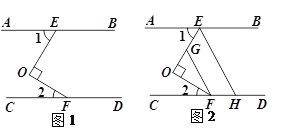
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
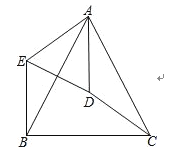
(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是 .

相关试题

