【题目】如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
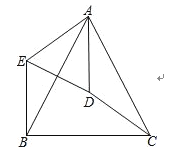
(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
参考答案:
【答案】(1)△AED∽△ABC;
(2)四边形AEBD是菱形.
【解析】
试题分析:(1)由旋转性质可得∠DAE=∠CAB、AE=AD,结合AB=AC根据![]() 且∠DAE=∠CAB可证得;
且∠DAE=∠CAB可证得;
(2)由三角形外心可得DB=DA=DC,结合△ADC≌△AEB知DB=DA=BE=AE,即可判定四边形AEBD的形状.
试题解析:(1)∵△ADC 绕点A顺时针旋转得到△AEB,
∴△ADC≌△AEB.
∴∠BAE=∠CAD,AE=AD.
∴∠DAE=∠CAB.
∵AB=AC,
∴![]() .
.
∴△AED∽△ABC.
(2)四边形AEBD是菱形.
∵D是△ABC的外心,
∴DB=DA=DC.
又∵△ADC≌△AEB,
∴AE=AD,BE=DC.
∴DB=DA=BE=AE.
∴四边形AEBD是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算x2-2x2的结果是()
A. -1 B. -x4 C. -x2 D. x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
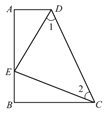
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
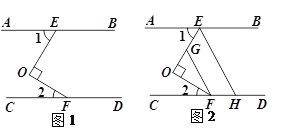
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2-9=0的根是_____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形三条边大小之间存在一定的关系,以下列各组线段为边,能组成三角形的是( )
A.2cm、3cm、5cm
B.5cm、6cm、10cm
C.1cm、1cm、3cm
D.3cm、4cm、9cm
相关试题

