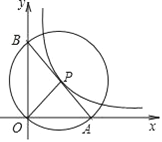
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
参考答案:
【答案】(1)证明见解析;(2)S△AOB=24.
【解析】试题分析:(1)、根据直角所对的弦为直径得出AB为直径,从而得出点P为中点;(2)、设P的坐标为(m,n),根据线段中点的性质得出OA=2m,OB=2n,最后根据面积的计算法则得出面积.
试题解析:(1)、证明:∵点A、O、B在⊙P上,且∠AOB=90°,
∴AB为⊙P直径, 即P为AB中点;
(2)、解:∵P为![]() (x>0)上的点,
(x>0)上的点,
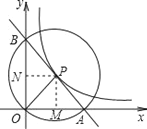
设点P的坐标为(m,n),则mn=12, 过点P作PM⊥x轴于M,PN⊥y轴于N,
∴M的坐标为(m,0),N的坐标为(0,n),且OM=m,ON=n,∵点A、O、B在⊙P上,
∴M为OA中点,OA=2 m;N为OB中点,OB=2 n, ∴S△AOB=![]() OAO B=2mn=24.
OAO B=2mn=24.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是
 的一张纸条,按图
的一张纸条,按图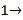 图
图 图
图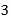 ,把这一纸条先沿
,把这一纸条先沿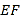 折叠并压平,再沿
折叠并压平,再沿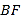 折叠并压平,若图3中
折叠并压平,若图3中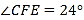 ,则图2中
,则图2中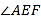 的度数为( )
的度数为( )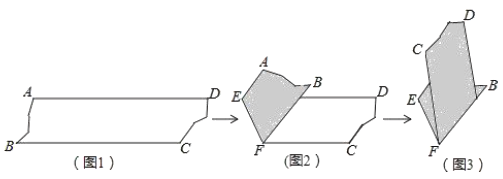
A.
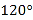 B.
B.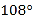 C.
C.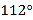 D.
D.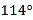
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控等手段引导市民节约用水。某市规定如下用水收费标准:每月每户的用水不超过6
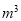 时,水费按正常收费;超过6
时,水费按正常收费;超过6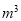 时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9
时,超过的部分收较高水费。该市某户居民今年2月份的用水量为9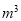 ,缴纳水费为27元;3月份的用水量为11
,缴纳水费为27元;3月份的用水量为11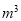 ,缴纳水费为37元。
,缴纳水费为37元。(1)求在限定量以内每吨多少元?超出部分的水费每吨多少元?
(2)若该市某居民今年4月份的用水量为13
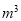 . 则应缴纳水费多少元?
. 则应缴纳水费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
-
科目: 来源: 题型:
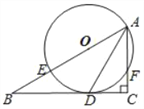
查看答案和解析>>【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=60°,AB=1,现将△ABC绕点A逆时针旋转至点B恰好落在BC上的B'处,其中点C运动路径为
 ,则图中阴影部分的面积是_____.
,则图中阴影部分的面积是_____.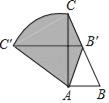
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)
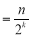 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________.
相关试题

