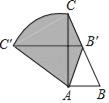
【题目】如图,在Rt△ABC中,∠B=60°,AB=1,现将△ABC绕点A逆时针旋转至点B恰好落在BC上的B'处,其中点C运动路径为![]() ,则图中阴影部分的面积是_____.
,则图中阴影部分的面积是_____.
参考答案:
【答案】![]()
【解析】分析:根据直角三角形的性质分别求出BC、AC,根据旋转变换的性质得到∠CAC′=60°,AC′=AC=![]() ,AB′=AB,根据三角形面积公式、扇形面积公式计算.
,AB′=AB,根据三角形面积公式、扇形面积公式计算.
详解:Rt△ABC中,∠B=60°,AB=1,
∴BC=2AB=2,AC=![]() AB=
AB=![]() ,
,
由旋转的性质可知,∠CAC′=60°,AC′=AC=![]() ,AB′=AB,
,AB′=AB,
∴△AB′B为等边三角形,
∴BB′=1,即B′是BC的中点,
∴S△AB′C=![]() S△ABC=
S△ABC=![]() ×1×
×1×![]() ×
×![]() =
=![]() ,
,
S扇形C′AC=![]() ,
,
∴图中阴影部分的面积=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数
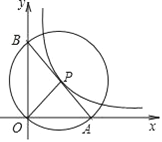
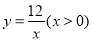 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
-
科目: 来源: 题型:
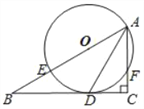
查看答案和解析>>【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F”运算:①当n为奇数时,F(n)=3n+1;②当n为偶数时,F(n)
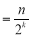 (其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则:
(其中k是使F(n)为奇数的正整数)……,两种运算交替重复进行,例如,取n=13,则: 若n=24,则第100次“F”运算的结果是________.
若n=24,则第100次“F”运算的结果是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x2+3xy-2x-1,B=-x2+xy-1,且3A+6B的值与x无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,任意一个正整数n都可以进行这样的分解:
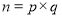 (p,q是正整数,且
(p,q是正整数,且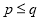 ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定: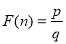 .
.例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=
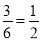 .
.(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为
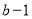 ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;(3)在(2)所得“和谐数”中,求F(t)的最大值.
相关试题

