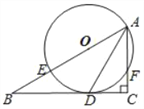
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
参考答案:
【答案】(1)证明见解析;(2)![]()
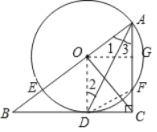
【解析】试题分析:(1)连接OD,由 OD=OA,可得∠1=∠2,再由BC为⊙O的切线,根据切线的性质可得∠ODB=90°,已知∠C=90°,所以∠ODB=∠C,即可判定OD∥AC,根据平行线的性质可得∠3=∠2,所以∠1=∠3,即可判定AD是∠BAC的平分线;(2)连接DF,已知∠B=30°,可求得∠BAC=60°,再由AD是∠BAC的平分线,可得∠3=30°,已知BC是⊙O的切线,根据弦切角定理可得∠FDC=∠3=30°,所以CD=![]() CF=
CF=![]() ,同理可得AC=
,同理可得AC=![]() CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=
CD=3,所以AF=2,过O作OG⊥AF于G,由垂径定理可得GF=![]() AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=
AF=1,四边形ODCG是矩形,所以CG=2,OG=CD=![]() ,由勾股定理可得OC=
,由勾股定理可得OC=![]() .
.
试题解析:
(1)证明:连接OD,∴OD=OA,∴∠1=∠2,
∵BC为⊙O的切线,∴∠ODB=90°,∵∠C=90°,∴∠ODB=∠C,∴OD∥AC,
∴∠3=∠2,∴∠1=∠3,∴AD是∠BAC的平分线;
(2)解:连接DF,∵∠B=30°,∴∠BAC=60°,
∵AD是∠BAC的平分线,∴∠3=30°,∵BC是⊙O的切线,∴∠FDC=∠3=30°,
∴CD=![]() CF=
CF=![]() ,∴AC=
,∴AC=![]() CD=3,∴AF=2,
CD=3,∴AF=2,
过O作OG⊥AF于G,∴GF=AF=1,四边形ODCG是矩形,
∴CG=2,OG=CD=![]() ,∴OC=
,∴OC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“等角的补角相等”的条件是________,结论是________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:4(x﹣3)(x+2)﹣(2x+3)(2x﹣3),其中x=﹣2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简与求值:
(
 )已知当
)已知当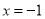 时,代数式
时,代数式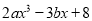 值为
值为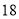 ,求代数式
,求代数式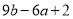 的值.
的值.(
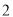 )已知
)已知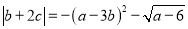 ,代数式
,代数式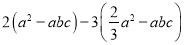 的值.
的值.(
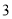 )若多项式
)若多项式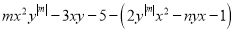 是关于
是关于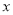 ,
, 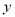 的四次二项式,求代数式
的四次二项式,求代数式 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果xm+1与xn是同类项,那么m﹣n=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列因式分解的过程,再回答提出的问题:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(1+x)]=(1+x)(1+x)2=(1+x)3,若分解1+x+x(1+x)+x(1+x)2+…+x(1+x)2017结果是_____.
-
科目: 来源: 题型:
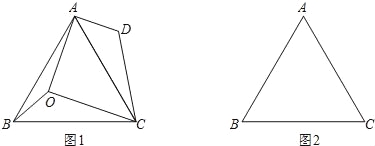
查看答案和解析>>【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
相关试题

