【题目】如图,在平面直角坐标系xOy中,抛物线y= ![]() +bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
A.![]()
B.![]()
C.2
D.![]()
参考答案:
【答案】B
【解析】∵抛物线y= ![]() +bx+c与x轴只有一个交点,∴△=
+bx+c与x轴只有一个交点,∴△= ![]() ﹣4ac=0,∴
﹣4ac=0,∴ ![]() ﹣4c=0,则有
﹣4c=0,则有 ![]() +bx+c=m两根的差为3,可得:
+bx+c=m两根的差为3,可得: ![]() ﹣4(c﹣m)=9,解得:m=
﹣4(c﹣m)=9,解得:m= ![]() .
.
所以答案是:B.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线
 与x轴,y轴分别交于点A,B,将
与x轴,y轴分别交于点A,B,将 沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为______.
沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.


(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 +bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:①ac>0;②方程ax2+bx+c=0的两根是
+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:①ac>0;②方程ax2+bx+c=0的两根是  =﹣1,
=﹣1,  =3;③2a﹣b=0;④当x>1时,y随x的增大而减小;则以上结论中正确的有( ).
=3;③2a﹣b=0;④当x>1时,y随x的增大而减小;则以上结论中正确的有( ).
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为44,且DE=6,则sin∠ODE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AD是BC边上的高,BD=3,CD=1,AD=2,P、Q、R分别是BC、AB、AC边上的动点,则△PQR周长的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
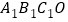 ,
,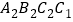 ,
,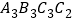 ,
, 按如图的方式放置
按如图的方式放置 点
点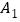 ,
,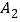 ,
,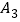 ,
, 和点,
和点, ,
,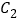 ,
,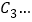 分别在直线
分别在直线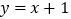 和x轴上,则点
和x轴上,则点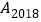 的坐标是______.
的坐标是______.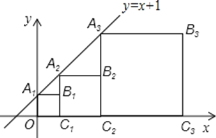
相关试题

