【题目】△ABC中,AD是BC边上的高,BD=3,CD=1,AD=2,P、Q、R分别是BC、AB、AC边上的动点,则△PQR周长的最小值为 .
参考答案:
【答案】![]()
【解析】如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,
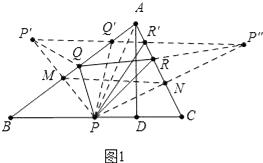
此时△PQ′R′的周长最小,这个最小值=P′P″,
∵PM=MP′,PN=NP″,
∴P′P″=2MN,
∴当MN最小时P′P″最小.如图2中,
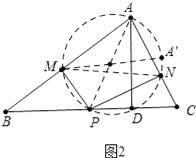
∵∠AMP=∠ANP=90°,
∴A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,
∵∠MAN是定值,
∴直径AP最小时,弦MN最小,
∴当点P与点D重合时,PA最小,此时MN最小.
如图3中,

∵在RT△ABD中,∠ADB=90°,AD=2,DB=3,
∴AB= ![]() ,在RT△ADC中,
,在RT△ADC中,
∵∠ADC=90°,AD=2,CD=1,
∴AC= ![]() ,
,
∵DM⊥AB,DN⊥AC,
∴ ![]() ACDN=
ACDN= ![]() DCAD,
DCAD,
∴DN= ![]() ,AN=
,AN= ![]() ,
,
∵∠MAD=∠DAB,∠AMD=∠ADB,
∴△AMD∽△ADB,∴ ![]() ,
,
∴ ![]() =AMAB,同理
=AMAB,同理 ![]() =ANAC,
=ANAC,
∴AMAB=ANAC,
∴ ![]() ,
,
∵∠MAN=∠CAB,∴△AMN∽△ACB,
∴ ![]() ,
,
∴ ![]() ,
,
∴MN= ![]() ,
,
∴△PQR周长的最小值=P′P″=2MN= ![]() .
.
故答案为: ![]() .
.
如图1中,作P点关于AB的对称点P′,作P点关于AC的对称点P″,连接P′P″,与AB交于点Q′,与AC交于点R′,连接PP′交AB于M,连接PP″交AC于N,此时△PQ′R′的周长最小,这个最小值=P′P″,然后证出P′P″=2MN,当MN最小时P′P″最小.如图2中, 根据圆周角定理得出A、M、P、N四点共圆,线段AP就是圆的直径,MN是弦,又由于∠MAN是定值,故直径AP最小时,弦MN最小,从而知道当点P与点D重合时,PA最小,此时MN最小,如图3中,首先根据勾股定理得出AB,AC的长度,然后根据面积法得出DN长,再根据勾股定理算出AN的长,进而判断出△AMD∽△ADB,根据相似三角形的性质得出 A D 2 =AMAB,同理 A D 2 =ANAC,故AMAB=ANAC,从而再判断出△AMN∽△ACB,根据相似三角形的性质得出MN的长,从而得出答案。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 +bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:①ac>0;②方程ax2+bx+c=0的两根是
+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:①ac>0;②方程ax2+bx+c=0的两根是  =﹣1,
=﹣1,  =3;③2a﹣b=0;④当x>1时,y随x的增大而减小;则以上结论中正确的有( ).
=3;③2a﹣b=0;④当x>1时,y随x的增大而减小;则以上结论中正确的有( ).
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,抛物线y=
 +bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( ).
A.
B.
C.2
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为44,且DE=6,则sin∠ODE= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形
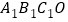 ,
,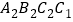 ,
,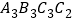 ,
, 按如图的方式放置
按如图的方式放置 点
点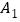 ,
,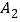 ,
,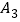 ,
, 和点,
和点, ,
,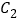 ,
,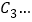 分别在直线
分别在直线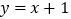 和x轴上,则点
和x轴上,则点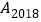 的坐标是______.
的坐标是______.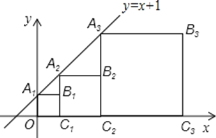
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位数比十位数大2,若把各位数字和十位数字对调,则所得的新的两位数比原数的两倍少17.若设原数的个位数为
 ,十位数字为
,十位数字为 ,则下列方程组正确的是( )
,则下列方程组正确的是( )A.
 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究性学习小组为了解同学们上学年参加社会实践活动的天数,随机抽查了该市部分八年级学生,来了解上学年参加社会实践活动的天数,并用得到的数据绘制了如图两幅不完整的统计图
 请你根据图中提供的信息问答下列问题:
请你根据图中提供的信息问答下列问题: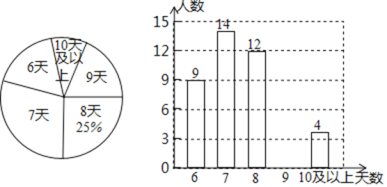
 本次共抽查了多少人?
本次共抽查了多少人? 补全条形统计图.
补全条形统计图. 在这次调查中,参加社会实践活动天数的众数和中位数分别是多少?
在这次调查中,参加社会实践活动天数的众数和中位数分别是多少? 如果本区市共有八年级学生14400人,请你估计“参加社会实践活动时间不少于9天”的有多少人?
如果本区市共有八年级学生14400人,请你估计“参加社会实践活动时间不少于9天”的有多少人?
相关试题

