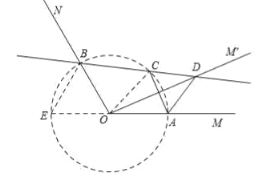
【题目】如图,已知![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,将射线
,将射线![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() ,旋转角为
,旋转角为![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,画直线
,画直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,有下列结论:
,有下列结论:
①![]() ; ②
; ②![]() 的大小随着
的大小随着![]() 的变化而变化;
的变化而变化;
③当![]() 时,四边形
时,四边形![]() 为菱形; ④
为菱形; ④![]() 面积的最大值为
面积的最大值为![]() ;
;

其中正确的是_____________.(把你认为正确结论的序号都填上).
参考答案:
【答案】①③④
【解析】
①根据对称的性质:对称点的连线被对称轴垂直平分可得:OM'是AC的垂直平分线,再由垂直平分线的性质可作判断;
②作⊙O,根据四点共圆的性质得:∠ACD=∠E=60°,说明∠ACD是定值,不会随着α的变化而变化;
③当α=30°时,即∠AOD=∠COD=30°,证明△AOC是等边三角形和△ACD是等边三角形,得OC=OA=AD=CD,可作判断;
④先证明△ACD是等边三角形,当AC最大时,△ACD的面积最大,当AC为直径时最大,根据面积公式计算后可作判断.
解:①∵A、C关于直线OM'对称,
∴OM'是AC的垂直平分线,
∴CD=AD,
故①正确;
②连接OC,由①知:OM'是AC的垂直平分线,
∴OC=OA,
∴OA=OB=OC,
以O为圆心,以OA为半径作⊙O,交AO的延长线于E,连接BE,
则A、B、C都在⊙O上,
∵∠MON=120°,
∴∠BOE=60°,
∵OB=OE,
∴△OBE是等边三角形,
∴∠E=60°,
∵A、C、B、E四点共圆,
∴∠ACD=∠E=60°,
故②不正确;
③当α=30°时,即∠AOD=∠COD=30°,
∴∠AOC=60°,
∴△AOC是等边三角形,
∴∠OAC=60°,OC=OA=AC,
由①得:CD=AD,
∴∠CAD=∠ACD=∠CDA=60°,
∴△ACD是等边三角形,
∴AC=AD=CD,
∴OC=OA=AD=CD,
∴四边形OADC为菱形,
故③正确;
④∵CD=AD,∠ACD=60°,
∴△ACD是等边三角形,
当AC最大时,△ACD的面积最大,
∵AC是⊙O的弦,即当AC为直径时最大,此时AC=2OA=2a,α=90°,
∴△ACD面积的最大值是:![]() AC2=
AC2=![]() ,
,
故④正确;
所以本题结论正确的有:①③④,
故答案为:①③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春
出发时间
到站时间
里程(km)
普通车
7:00
11:00
300
快车
7:30
10:30
300
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
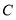 在线段
在线段 上,图中共有三条线段
上,图中共有三条线段 ,
,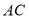 和
和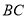 ,若其中有一条线段的长度是另外一条线段长度的2倍,则称点
,若其中有一条线段的长度是另外一条线段长度的2倍,则称点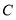 是线段
是线段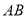 的“巧点”.
的“巧点”.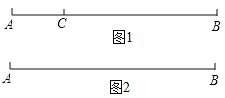
(1)线段的中点_________这条线段的“巧点”;(填“是”或“不是”);
(2)如图2,已知
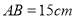 .动点
.动点 从点
从点 出发,以
出发,以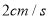 的速度沿
的速度沿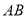 向点
向点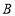 匀速运动;点
匀速运动;点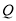 从点
从点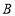 出发,以
出发,以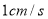 的速度沿
的速度沿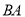 向点
向点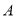 匀速运动,点
匀速运动,点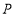 ,
,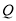 同时出发,当其中一点到达终点时,运动停止.设移动的时间为
同时出发,当其中一点到达终点时,运动停止.设移动的时间为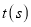 ,当
,当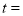 _________
_________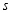 时,
时,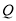 为
为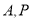 的“巧点”.
的“巧点”. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
 ÷7;
÷7;(2)
 ;
;(3)
 ;
;(4)
 ;
;(5)

-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解答下列问题:

(1)义乌市为了搞好“五水共治”工作,将一段长为
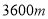 的河道任务交由甲乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治
的河道任务交由甲乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治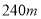 ,乙工程队每天整治
,乙工程队每天整治 ,试求甲乙两个工程队分别整治了多长的河道.
,试求甲乙两个工程队分别整治了多长的河道.(2)小玲在数学书上发现如图所示的题目,两个方框表示的是同一个数,请你帮小玲求出方框所表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x -2mx(m为常数),当-1≤x≤2时,函数y的最小值为-2,则m的值是( )
A.
 B.
B.  C.
C.  或
或 D. -
D. - 或
或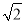
相关试题

