【题目】计算:
(1)![]() ÷7;
÷7;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]()
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)-1;(5)
;(4)-1;(5)![]()
【解析】
利用有理数的混合运算法则和乘法分配律、结合律计算即可完成.
(1)(-28![]() +14
+14![]() )÷7;
)÷7;
解:原式=(-28![]() +14
+14![]() )×
)×![]()
![]()
=-4![]() +2
+2![]()
=-2![]() .
.
(2)(-13![]() )÷5-1
)÷5-1![]() ÷5+13×
÷5+13×![]() ;
;
解:原式=(-13![]() )×
)×![]() -1
-1![]() ×
×![]() +13×
+13×![]()
=(-13![]() -1
-1![]() +13)×
+13)×![]()
=-2×![]()
=-![]() .
.
(3)1![]() ×[3×(-
×[3×(-![]() )-1]-
)-1]-![]() ×(-8)-8;
×(-8)-8;
解:原式=![]() ×(-2-1)+
×(-2-1)+![]() -8
-8
=-![]() +
+![]() -8
-8
=-![]() .
.
(4)-|-![]() |-|-
|-|-![]() ×
×![]() |-|
|-|![]() -
-![]() |;
|;
解:原式=-![]() -
-![]() -(
-(![]() -
-![]() )
)
=-![]() -
-![]() -
-![]() +
+![]()
=-1.
(5)(2![]() -3
-3![]() +
+![]() )÷(-1
)÷(-1![]() )+(-1
)+(-1![]() )÷(2
)÷(2![]() -3
-3![]() +
+![]() ).
).
解:因为(2![]() -3
-3![]() +
+![]() )÷(-1
)÷(-1![]() )
)
=(![]() -
-![]() +
+![]() )×(-
)×(-![]() )
)
=![]() ×(-
×(-![]() )-
)-![]() ×(-
×(-![]() )+
)+![]() ×(-
×(-![]() )
)
=-2+3-![]()
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某客运站行车时刻表如图,若全程保持匀速行驶,则当快车出发______小时后,两车相距25km.
哈尔滨—长春
出发时间
到站时间
里程(km)
普通车
7:00
11:00
300
快车
7:30
10:30
300
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
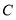 在线段
在线段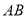 上,图中共有三条线段
上,图中共有三条线段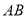 ,
,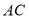 和
和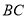 ,若其中有一条线段的长度是另外一条线段长度的2倍,则称点
,若其中有一条线段的长度是另外一条线段长度的2倍,则称点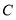 是线段
是线段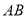 的“巧点”.
的“巧点”.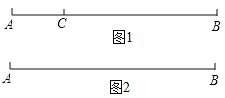
(1)线段的中点_________这条线段的“巧点”;(填“是”或“不是”);
(2)如图2,已知
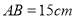 .动点
.动点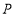 从点
从点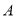 出发,以
出发,以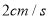 的速度沿
的速度沿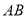 向点
向点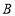 匀速运动;点
匀速运动;点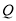 从点
从点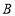 出发,以
出发,以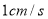 的速度沿
的速度沿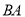 向点
向点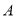 匀速运动,点
匀速运动,点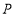 ,
,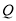 同时出发,当其中一点到达终点时,运动停止.设移动的时间为
同时出发,当其中一点到达终点时,运动停止.设移动的时间为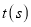 ,当
,当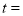 _________
_________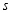 时,
时,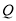 为
为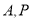 的“巧点”.
的“巧点”. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 分别在
分别在 上,且
上,且 ,将射线
,将射线 绕点
绕点 逆时针旋转得到
逆时针旋转得到 ,旋转角为
,旋转角为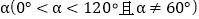 ,作点
,作点 关于直线
关于直线 的对称点
的对称点 ,画直线
,画直线 交
交 于点
于点 ,连接
,连接 ,
, ,有下列结论:
,有下列结论:①
 ; ②
; ② 的大小随着
的大小随着 的变化而变化;
的变化而变化;③当
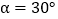 时,四边形
时,四边形 为菱形; ④
为菱形; ④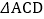 面积的最大值为
面积的最大值为 ;
;
其中正确的是_____________.(把你认为正确结论的序号都填上).
-
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解答下列问题:

(1)义乌市为了搞好“五水共治”工作,将一段长为
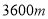 的河道任务交由甲乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治
的河道任务交由甲乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治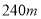 ,乙工程队每天整治
,乙工程队每天整治 ,试求甲乙两个工程队分别整治了多长的河道.
,试求甲乙两个工程队分别整治了多长的河道.(2)小玲在数学书上发现如图所示的题目,两个方框表示的是同一个数,请你帮小玲求出方框所表示的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x -2mx(m为常数),当-1≤x≤2时,函数y的最小值为-2,则m的值是( )
A.
 B.
B.  C.
C.  或
或 D. -
D. - 或
或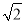
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(0,3),C(1,0).
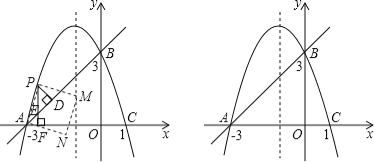
(1)求此抛物线的解析式.
(2)点P是直线AB上方的抛物线上一动点,(不与点A、B重合),过点P作x轴的垂线,垂足为F,交直线AB于点E,作PD⊥AB于点D.
①动点P在什么位置时,△PDE的周长最大,求出此时P点的坐标;
②连接PA,以AP为边作图示一侧的正方形APMN,随着点P的运动,正方形的大小、位置也随之改变.
当顶点M或N恰好落在抛物线对称轴上时,求出对应的P点的坐标.(结果保留根号)
相关试题

