【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】C
【解析】试题分析:①利用线段垂直平分线的性质的逆定理可得结论;②证△OMB≌△OEB得△EOB≌△CMB;
③先证△BEF是等边三角形得出BF=EF,再证DEBF得出DE=BF,所以得DE=EF;④由②可知△BCM≌△BEO,则面积相等,△AOE和△BEO属于等高的两个三角形,其面积比就等于两底的比,即S△AOE:S△BOE=AE:BE,由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE,得出结论S△AOE:S△BOE=AE:BE=1:2.
①∵矩形ABCD中,O为AC中点, ∴OB=OC, ∵∠COB=60°, ∴△OBC是等边三角形, ∴OB=BC,
∵FO=FC, ∴FB垂直平分OC, 故①正确;
②∵FB垂直平分OC, ∴△CMB≌△OMB, ∵OA=OC,∠FOC=∠EOA,∠DCO=∠BAO, ∴△FOC≌△EOA,
∴FO=EO, 易得OB⊥EF, ∴△OMB≌△OEB, ∴△EOB≌△CMB, 故②正确;
③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°,BF=BE, ∴△BEF是等边三角形, ∴BF=EF,
∵DF∥BE且DF=BE, ∴四边形DEBF是平行四边形, ∴DE=BF, ∴DE=EF, 故③正确;
④在直角△BOE中∵∠3=30°, ∴BE=2OE, ∵∠OAE=∠AOE=30°, ∴AE=OE, ∴BE=2AE,
∴S△AOE:S△BCM=S△AOE:S△BOE=1:2, 故④错误;
所以其中正确结论的个数为3个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】亚奥理事会于
 年
年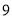 月3
月3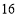 日在土库曼斯坦阿什哈巴德举行第
日在土库曼斯坦阿什哈巴德举行第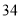 届代表大会,并在会上投票选出
届代表大会,并在会上投票选出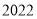 年第
年第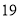 届亚运会举办城市为杭州.
届亚运会举办城市为杭州.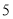 个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间
个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间 年
年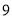 月
月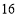 日
日 时应是( ).
时应是( ).
A.伦敦时间
 年
年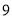 月
月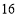 日
日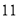 时
时B.巴黎时间
 年
年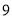 月
月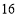 日
日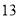 时
时C.智利时间
 年
年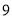 月
月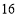 日
日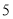 时
时D.曼谷时间
 年
年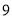 月
月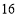 日
日 时
时 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2-2x+3的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作
y轴的平行线,与直线AC交于点G(点G在点F的上方).若,
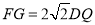
求点F的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】-4,|-2|,-2,-(-3.5),0,-

(1)在如图所示的数轴上表示出以上各数;

(2)比较以上各数的大小,用“<”号连接起来;
(3) 在以上各数中选择恰当的数填在下面这两个圈的重叠部分

-
科目: 来源: 题型:
查看答案和解析>>【题目】“安全教育,警钟长鸣”,为此某校从14 000名学生中随机抽取了200名学生就安全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图甲).
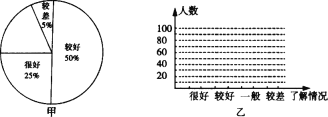
(1)补全扇形统计图,并计算这200名学生中对安全知识了解“较好”、“很好”的总人数;
(2)在图乙中,绘制样本频数的条形统计图;
(3)根据以上信息,请提出一条合理化建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=______________.
相关试题

