【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.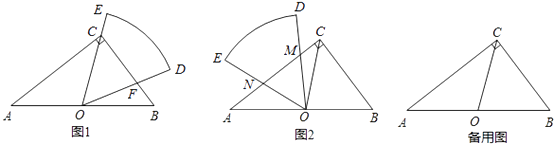
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
参考答案:
【答案】
(1)解:∵∠ACB=90°,点O是AB的中点,
∴OC=0B=OA=5.
∴∠OCB=∠B,∠ACO=∠A.
∵∠DOE=∠B,
∴∠FOC=∠OCF.
∴FC=FO.
∴△COF是等腰三角形.
过点F作FH⊥OC,垂足为H,如图1,
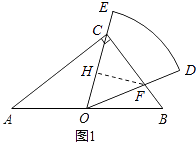
∵FC=FO,FH⊥OC,
∴CH=OH= ![]() ,∠CHF=90°.
,∠CHF=90°.
∵∠HCF=∠B,∠CHF=∠BCA=90°,
∴△CHF∽△BCA.
∴ ![]() =
= ![]() .
.
∵CH= ![]() ,AB=10,BC=6,
,AB=10,BC=6,
∴CF= ![]() .
.
∴CF的长为 ![]() .
.
(2)解:①若△OMN∽△BCO,如图2,
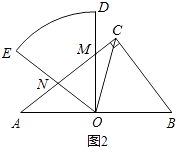
则有∠NMO=∠OCB.
∵∠OCB=∠B,
∴∠NMO=∠B.
∵∠A=∠A,
∴△AOM∽△ACB.
∴ ![]() =
= ![]() .
.
∵∠ACB=90°,AB=10,BC=6,
∴AC=8.
∵AO=5,AC=8,AB=10,
∴AM= ![]() .
.
∴CM=AC﹣AM= ![]() .
.
②若△OMN∽△BOC,如图3,
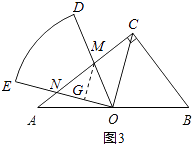
则有∠MNO=∠OCB.
∵∠OCB=∠B,
∴∠MNO=∠B.
∵∠ACO=∠A,
∴△CON∽△ACB.
∴ ![]() =
= ![]() =
= ![]() .
.
∵BC=6,AB=10,AC=8,CO=5,
∴ON= ![]() ,CN=
,CN= ![]() .
.
过点M作MG⊥ON,垂足为G,如图3,
∵∠MNO=∠B,∠MON=∠B,
∴∠MNO=∠MON.
∴MN=MO.
∵MG⊥ON,即∠MGN=90°,
∴NG=OG= ![]() .
.
∵∠MNG=∠B,∠MGN=∠ACB=90°,
∴△MGN∽△ACB.
∴ ![]() =
= ![]() .
.
∵GN= ![]() ,BC=6,AB=10,
,BC=6,AB=10,
∴MN= ![]() .
.
∴CM=CN﹣MN= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∴当CM的长是 ![]() 或
或 ![]() 时,△OMN与△BCO相似.
时,△OMN与△BCO相似.
【解析】(1)在直角三角形中由∠ACB=90°,点O是AB的中点,得到OC=0B=OA,∠OCB=∠B,∠ACO=∠A,由∠DOE=∠B,得到∠FOC=∠OCF,由等角对等边得到FC=FO,即△COF是等腰三角形;由FC=FO,FH⊥OC,得到CH=OH ,由∠HCF=∠B,∠CHF=∠BCA,得到△CHF∽△BCA,得到 比例,求出CF的长;(2)①若△OMN∽△BCO,则有对应角相等,即∠NMO=∠OCB,由∠OCB=∠B,得到∠NMO=∠B;再由∠A=∠A,得到△AOM∽△ACB,![]() 根据勾股定理由∠ACB=90°,求出AC=8,得到AM的值,即CM=AC﹣AM;②若△OMN∽△BOC,则有对应角相等∠MNO=∠OCB,由∠OCB=∠B,得到∠MNO=∠B,又因为∠ACO=∠A,所以△CON∽△ACB,得
根据勾股定理由∠ACB=90°,求出AC=8,得到AM的值,即CM=AC﹣AM;②若△OMN∽△BOC,则有对应角相等∠MNO=∠OCB,由∠OCB=∠B,得到∠MNO=∠B,又因为∠ACO=∠A,所以△CON∽△ACB,得![]() 到比例,求出ON
到比例,求出ON![]() 、CN的值;由∠MNO=∠MO,得到MN=MO,因为MG⊥ON,得到NG=OG,因为∠MNG=∠B,∠MGN=∠ACB,得到△MGN∽△ACB,得到比例 ,求出MN的值,得到CM=CN﹣MN,求出当CM的长是
、CN的值;由∠MNO=∠MO,得到MN=MO,因为MG⊥ON,得到NG=OG,因为∠MNG=∠B,∠MGN=∠ACB,得到△MGN∽△ACB,得到比例 ,求出MN的值,得到CM=CN﹣MN,求出当CM的长是 ![]() 或
或 ![]() 时,△OMN与△BCO相似.
时,△OMN与△BCO相似.
【考点精析】认真审题,首先需要了解直角三角形斜边上的中线(直角三角形斜边上的中线等于斜边的一半),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣
 +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2 , 求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
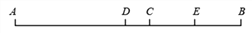
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=
 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.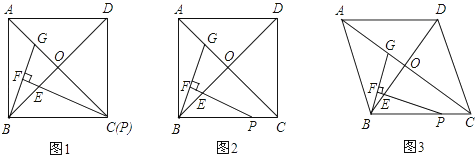
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: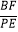 与
与  的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出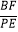 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
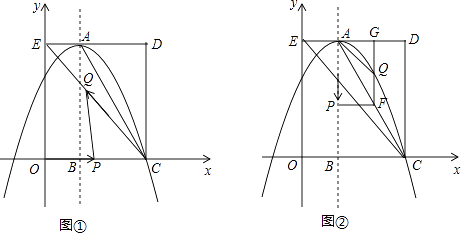
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=
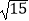 ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )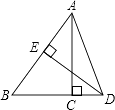
A.
B.
C.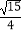
D.
相关试题

