【题目】某公园有一个抛物线形状的观景拱桥ABC,其横截面如图所示,在图中建立的直角坐标系中,抛物线的解析式为y=﹣ ![]() +c且过顶点C(0,5)(长度单位:m)
+c且过顶点C(0,5)(长度单位:m)
(1)直接写出c的值;
(2)现因搞庆典活动,计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯,地毯的价格为20元/m2 , 求购买地毯需多少元?
(3)在拱桥加固维修时,搭建的“脚手架”为矩形EFGH(H、G分别在抛物线的左右侧上),并铺设斜面EG.已知矩形EFGH的周长为27.5m,求斜面EG的倾斜角∠GEF的度数.(精确到0.1°)
参考答案:
【答案】
(1)解:抛物线的解析式为y=﹣ ![]() +c,
+c,
∵点(0,5)在抛物线上
∴c=5;
(2)解:由(1)知,OC=5,
令y=0,即﹣ ![]() +5=0,解得x1=10,x2=﹣10;
+5=0,解得x1=10,x2=﹣10;
∴地毯的总长度为:AB+2OC=20+2×5=30,
∴30×1.5×20=900
答:购买地毯需要900元
(3)解:可设G的坐标为(m,﹣ ![]() +5)其中m>0
+5)其中m>0
则EF=2m,GF=﹣ ![]() +5,
+5,
由已知得:2(EF+GF)=27.5,
即2(2m﹣ ![]() +5)=27.5,
+5)=27.5,
解得:m1=5,m2=35(不合题意,舍去),
把m1=5代入,﹣ ![]() +5=﹣
+5=﹣ ![]() ×52+5=3.75,
×52+5=3.75,
∴点G的坐标是(5,3.75),
∴EF=10,GF=3.75,
在Rt△EFG中,tan∠GEF= ![]() =
= ![]() =0.375,
=0.375,
∴∠GEF≈20.6°.
【解析】(1)根据二次函数的实际应用,顶点C(0,5)在抛物线上,直接得到c=5;(2)由(1)知,OC=5,抛物线的值是0,得到一元二次方程﹣![]() x2 +5=0,求出地毯的总长度为AB+2OC=30;(3)根据图像知2(EF+GF)=27.5,得到点G的坐标是(5,3.75),得到EF=10,GF=3.75,在Rt△EFG中,tan∠GEF= GF: EF =
x2 +5=0,求出地毯的总长度为AB+2OC=30;(3)根据图像知2(EF+GF)=27.5,得到点G的坐标是(5,3.75),得到EF=10,GF=3.75,在Rt△EFG中,tan∠GEF= GF: EF =![]() ,求出∠GEF≈20.6°;此题是综合题,难度较大,计算和解方程时需认真仔细.
,求出∠GEF≈20.6°;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
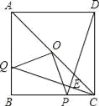
查看答案和解析>>【题目】如图,AC是正方形ABCD的对角线,点O是AC的中点,点Q是AB上一点,连接CQ,DP⊥CQ于点E,交BC于点P,连接OP,OQ;
求证:(1)△BCQ≌△CDP;(2)OP=OQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为2a ,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
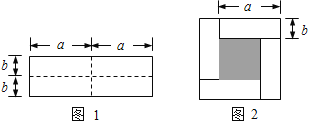
(1)图2的阴影部分的正方形的边长是 ______.
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)
 = _____________;
= _____________; (方法2)
 =______________;
=______________;(3)观察如图2,写出(a+b)2,(a-b)2,ab这三个代数式之间的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
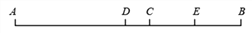
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.
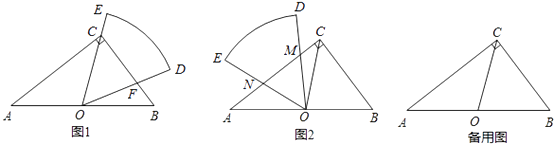
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似?
相关试题

