【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.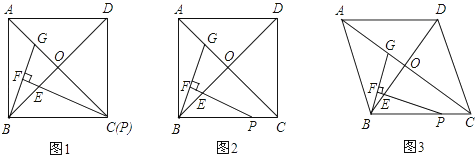
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: ![]() 与
与 ![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出 ![]() 的值.
的值.
参考答案:
【答案】
(1)证明:∵四边形ABCD是正方形,P与C重合,
∴OB=OP,∠BOC=∠BOG=90°,
∵PF⊥BG,∠PFB=90°,
∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO,
∴∠GBO=∠EPO,
在△BOG和△POE中, 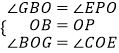
∴△BOG≌△POE(ASA);
(2)解:猜想 ![]() =
= ![]() .
.
证明:如图2,过P作PM∥AC交BG于M,交BO于N,
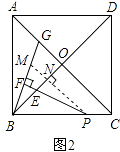
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中, 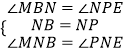
∴△BMN≌△PEN(ASA),
∴BM=PE.
∵∠BPE= ![]() ∠ACB,∠BPN=∠ACB,
∠ACB,∠BPN=∠ACB,
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中, 
∴△BPF≌△MPF(ASA).
∴BF=MF.
即BF= ![]() BM.
BM.
∴BF= ![]() PE.
PE.
即 ![]() =
= ![]() ;
;
故答案为 ![]() ;
;
(3)解:如图3,
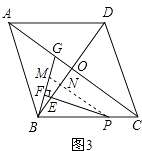
过P作PM∥AC交BG于点M,交BO于点N,
∴∠BPN=∠ACB=α,∠PNE=∠BOC=90°,
在Rt△BOC中,OC= ![]() AC=4,OB=
AC=4,OB= ![]() BD=3,
BD=3,
∴tan∠ACB= ![]() =
= ![]()
由(2)同理可得:BF= ![]() BM,∠MBN=∠EPN,
BM,∠MBN=∠EPN,
∵∠BNM=∠PNE=90°,
∴△BMN∽△PEN.
∴ ![]() .
.
在Rt△BNP中,tan∠ACB= ![]() =
= ![]() ,
,
∴ ![]() =tan∠ACB=
=tan∠ACB= ![]() .
.
即 ![]() =
= ![]() .
.
∴ ![]() =
= ![]() ×
× ![]() =
= ![]() .
.
【解析】(1)先依据正方形的性质以及P与C重合,可证明OB=OP,∠BOC=∠BOG=90°,由同角的余角相等可得到∠GBO=∠EPO,然后依据ASA可得到△BOG≌△POE;
(2)过P作PM∥AC交BG于M,交BO于N,然后依据ASA可证明△BMN≌△PEN、△BPF≌△MPF(ASA),从而可得到BM=PE,BF=![]() BM.则可求得
BM.则可求得 ![]() 的值;
的值;
(3)过P作PM∥AC交BG于点M,交BO于点N,由(2)可知到BF=![]() ,∠MBN=∠EPN,然后再可证明△BMN∽△PEN,然后由相似三角形的对应边成比例求解即可.
,∠MBN=∠EPN,然后再可证明△BMN∽△PEN,然后由相似三角形的对应边成比例求解即可.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣
 ;
;②由5=2﹣x移项得x=5﹣2;
③由
 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
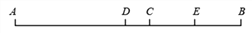
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.
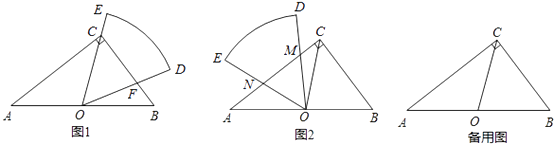
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
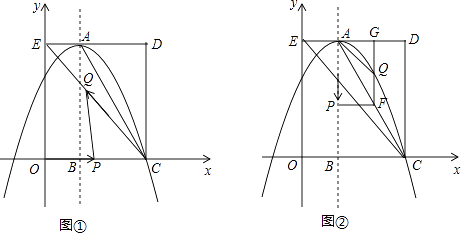
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=
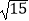 ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )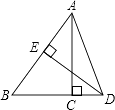
A.
B.
C.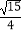
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.

相关试题

