搜索
【题目】下列各式中：
①由3x＝﹣4系数化为1得x＝﹣
；
②由5＝2﹣x移项得x＝5﹣2；
③由
去分母得2（2x﹣1）＝1+3（x﹣3）；
④由2（2x﹣1）﹣3（x﹣3）＝1去括号得4x﹣2﹣3x﹣9＝1．
其中正确的个数有（ ）
A. 0个 B. 1个 C. 3个 D. 4个
参考答案：
【答案】A
【解析】
根据解一元一次方程的去分母、去括号、移项及系数化1的方法依次判断后即可解答.
①由3x=﹣4系数化为1得x=﹣
，可知①错误；
②由5=2﹣x移项得x=2﹣5，可知②错误；
③由
去分母得2（2x﹣1）=6+3（x﹣3），可知③错误；
④由2（2x﹣1）﹣3（x﹣3）=1去括号得4x﹣2﹣3x+9=1，可知④错误．
综上，正确的结论有0个，故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）2x（x+1）﹣（x+2）（x﹣2）+（x﹣1）2
（2）（x﹣1﹣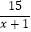
） 
． -
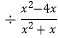科目： 来源： 题型：
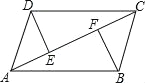
查看答案和解析>>【题目】已知DE⊥AC，BF⊥AC，垂足分别是E、F，AE=CF，DC∥AB，
（1）试证明：DE=BF；
（2）连接DF、BE，猜想DF与BE的关系？
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
（2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=
,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.
-
科目： 来源： 题型：
查看答案和解析>>【题目】A，B两地相距2400米，甲、乙两人分别从A，B两地同时出发相向而行，乙的速度是甲的2倍，已知乙到达A地15分钟后甲到达B地．
（1）求甲每分钟走多少米？
（2）两人出发多少分钟后恰好相距480米？
-
科目： 来源： 题型：
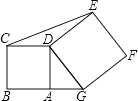
查看答案和解析>>【题目】如图，点A在线段BG上，四边形ABCD和四边形DEFG都是正方形，面积分别是10和19，则△CDE的面积为_____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】一件工程甲独做50天可完，乙独做75天可完，现在两个人合作，但是中途乙因事离开几天，从开工后40天把这件工程做完，则乙中途离开了（ ）天．
A. 10 B. 20 C. 30 D. 25
相关试题
