【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.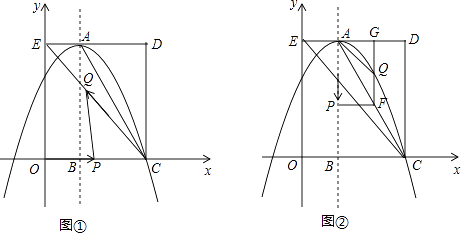
(1)填空:点A坐标为;抛物线的解析式为 .
(2)在图①中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图②中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?
参考答案:
【答案】
(1)(1,4),y=﹣(x﹣1)2+4
(2)解:依题意有:OC=3,OE=4,
∴CE= ![]() =
= ![]() =5,
=5,
当∠QPC=90°时,
∵cos∠QCP= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ;
;
当∠PQC=90°时,
∵cos∠QCP= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() .
.
∴当t= ![]() 或t=
或t= ![]() 时,△PCQ为直角三角形
时,△PCQ为直角三角形
(3)解:∵A(1,4),C(3,0),
设直线AC的解析式为y=kx+b,则
![]() ,
,
解得 ![]() .
.
故直线AC的解析式为y=﹣2x+6.
∵P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得x=1+ ![]() ,
,
∴Q点的横坐标为1+ ![]() ,
,
将x=1+ ![]() 代入y=﹣(x﹣1)2+4中,得y=4﹣
代入y=﹣(x﹣1)2+4中,得y=4﹣ ![]() .
.
∴Q点的纵坐标为4﹣ ![]() ,
,
∴QF=(4﹣ ![]() )﹣(4﹣t)=t﹣
)﹣(4﹣t)=t﹣ ![]() ,
,
∴S△ACQ=S△AFQ+S△CFQ
= ![]() FQAG+
FQAG+ ![]() FQDG
FQDG
= ![]() FQ(AG+DG)
FQ(AG+DG)
= ![]() FQAD
FQAD
= ![]() ×2(t﹣
×2(t﹣ ![]() )
)
=﹣ ![]() +t
+t
=﹣ ![]() (t2+4﹣4t﹣4)
(t2+4﹣4t﹣4)
=﹣ ![]() (t﹣2)2+1,
(t﹣2)2+1,
∴当t=2时,△ACQ的面积最大,最大值是1
【解析】解:(1)∵抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,
∴点A坐标为(1,4),
设抛物线的解析式为y=a(x﹣1)2+4,
把C(3,0)代入抛物线的解析式,可得a(3﹣1)2+4=0,
解得a=﹣1.
故抛物线的解析式为y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(1)由抛物线的对称轴为x=1,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4),点A在DE上,得到点A坐标为(1,4),设抛物线的解析式为y=a(x﹣1)2+4,把C(3,0)代入抛物线的解析式,求出a=﹣1,得到抛物线的解析式;(2)依题意有OC=3,OE=4,根据勾股定理CE=5,当∠QPC=90°时,cos∠QCP= PC: CQ = OC:CE,得到![]() =
=![]() , 解得t=
, 解得t=![]() ; 当∠PQC=90°时,由cos∠QCP= CQ: PC = OC: CE ,得到
; 当∠PQC=90°时,由cos∠QCP= CQ: PC = OC: CE ,得到![]() =
=![]() ,解得t=
,解得t=![]() ,当t=
,当t=![]() 或t=
或t=![]() 时,△PCQ为直角三角形;(3)把A(1,4),C(3,0),代入直线AC的解析式y=kx+b,得到直线AC的解析式为y=﹣2x+6,由P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得到Q点的横坐标为1+
时,△PCQ为直角三角形;(3)把A(1,4),C(3,0),代入直线AC的解析式y=kx+b,得到直线AC的解析式为y=﹣2x+6,由P(1,4﹣t),将y=4﹣t代入y=﹣2x+6中,得到Q点的横坐标为1+![]() ,Q点的纵坐标为4﹣
,Q点的纵坐标为4﹣![]() ,得到QF=4﹣
,得到QF=4﹣![]() ,所以S△ACQ=S△AFQ+S△CFQ,求出当t=2时,△ACQ的面积最大,最大值是1;此题是综合题,难度较大,计算和解方程时需认真仔细.
,所以S△ACQ=S△AFQ+S△CFQ,求出当t=2时,△ACQ的面积最大,最大值是1;此题是综合题,难度较大,计算和解方程时需认真仔细.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点 C 是线段 AB 上一点,且 5BC=2AB,D 是 AB 的中点,E 是CB 的中点,(1)若 DE=6,求 AB 的长;(2)求 AD:AC.
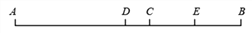
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,扇形纸片DOE的顶点O与边AB的中点重合,OD交BC于点F,OE经过点C,且∠DOE=∠B.
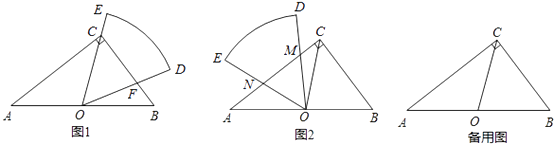
(1)证明△COF是等腰三角形,并求出CF的长;
(2)将扇形纸片DOE绕点O逆时针旋转,OD,OE与边AC分别交于点M,N(如图2),当CM的长是多少时,△OMN与△BCO相似? -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE=
 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.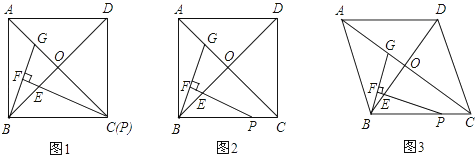
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: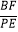 与
与  的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出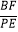 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=
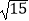 ,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )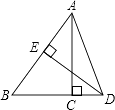
A.
B.
C.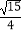
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.
(1)如图1,求证:AE⊥BF;
(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各式:
(1)解不等式
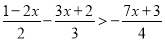 ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.(2)解方程组:
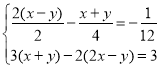 .
.
相关试题

