【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.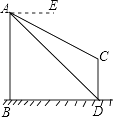
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
参考答案:
【答案】
(1)
解:根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)
解:延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AFtan∠FAC=60× ![]() =20
=20 ![]() ,
,
又∵FD=60,
∴CD=60﹣20 ![]() ,
,
∴建筑物CD的高度为(60﹣20 ![]() )米.
)米.
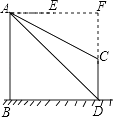
【解析】(1)根据题意得:BD∥AE,从而得到∠BAD=∠ADB=45°,利用BD=AB=60,求得两建筑物底部之间水平距离BD的长度为60米;(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,根据AF=BD=DF=60,在Rt△AFC中利用∠FAC=30°求得CF,然后即可求得CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 若AB=BC,则点B为线段AC的中点 B. 射线AB和射线BA是同一条射线
C. 两点之间的线段就是两点之间的距离 D. 同角的补角一定相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 ∥
∥ ,⊙O与
,⊙O与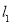 和
和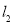 分别相切于点A和点B.直线MN与
分别相切于点A和点B.直线MN与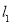 相交于M,与
相交于M,与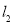 相交于N,⊙O的半径为1,∠1=60°,直线MN从如图所示位置向右平移,下列结论:①
相交于N,⊙O的半径为1,∠1=60°,直线MN从如图所示位置向右平移,下列结论:①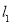 和
和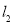 的距离为2;②MN=
的距离为2;②MN=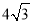 ;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=
;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=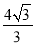 时,直线MN与⊙O相切.其中正确的序号是 .
时,直线MN与⊙O相切.其中正确的序号是 .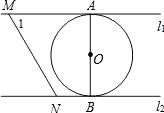
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣1时,代数式ax2+bx+1的值为﹣1,则(1+a﹣b)(1﹣a+b)的值为( )
A. ﹣3 B. ﹣1 C. 1 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
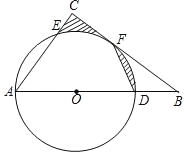
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣4x﹣5,则b= , c= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠A=90°,AB = AC,BD平分∠ABC。
求证:BC = AB + AD

相关试题

