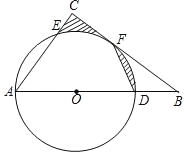
【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
参考答案:
【答案】(1)证明详见解析;(2) 4.
【解析】
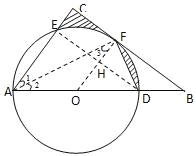
试题分析:(1)连接OF,AF,由题意得出![]() ,由圆周角定理和等腰三角形的性质得出∠1=∠3,证出AC∥OF,得出∠BFO=∠ACB=90°,即可得出结论;
,由圆周角定理和等腰三角形的性质得出∠1=∠3,证出AC∥OF,得出∠BFO=∠ACB=90°,即可得出结论;
(2)连接ED,交OF于H,由圆周角定理得出∠AED=90°,由勾股定理求出ED=8,证明四边形ECFH为矩形,得出∠EHO=90°,OF⊥ED,由三角形中位线定理得出OH=![]() =3,求出HF=5﹣3=2,得出
=3,求出HF=5﹣3=2,得出![]() =4,证出阴影部分的面积与△CEF的面积相等,即可得出答案.
=4,证出阴影部分的面积与△CEF的面积相等,即可得出答案.
试题解析:(1)连接OF,AF如图,
∵F为![]() 的中点,
的中点,
∴![]() ,
,
∴∠1=∠2,
∵AO=FO,
∴∠3=∠2,
∴∠1=∠3,
∴AC∥OF,
∴∠BFO=∠ACB=90°,
∵F为⊙O上一点,
∴BC为⊙O的切线;
(2)连接ED,交OF于H,如图,
∵AD为⊙O的直径,
∴∠AED=90°,
在Rt△ADE中,ED=![]() =8,
=8,
∵∠AED=90°=∠ACF=∠BFO,
∴四边形ECFH为矩形,
∴∠EHO=90°,OF⊥ED,
∴H为ED的中点,
∴EH=4,
∵O为AD的中点,
∴OH=![]() =3,
=3,
∴HF=5﹣3=2,
∴![]() =4,
=4,
∵![]() ,
,
∴弓形FD与弓形EF全等,
∴阴影部分的面积与△CEF的面积相等,
故图中阴影部分的面积为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
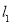 ∥
∥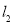 ,⊙O与
,⊙O与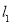 和
和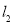 分别相切于点A和点B.直线MN与
分别相切于点A和点B.直线MN与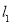 相交于M,与
相交于M,与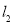 相交于N,⊙O的半径为1,∠1=60°,直线MN从如图所示位置向右平移,下列结论:①
相交于N,⊙O的半径为1,∠1=60°,直线MN从如图所示位置向右平移,下列结论:①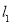 和
和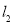 的距离为2;②MN=
的距离为2;②MN=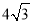 ;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=
;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=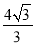 时,直线MN与⊙O相切.其中正确的序号是 .
时,直线MN与⊙O相切.其中正确的序号是 .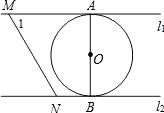
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣1时,代数式ax2+bx+1的值为﹣1,则(1+a﹣b)(1﹣a+b)的值为( )
A. ﹣3 B. ﹣1 C. 1 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
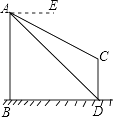
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣4x﹣5,则b= , c= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,∠A=90°,AB = AC,BD平分∠ABC。
求证:BC = AB + AD

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PB和PC是△ABC的两条外角平分线。
①求证:∠BPC=90°-
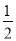 ∠BAC.
∠BAC.②根据第①问的结论猜想:三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?
相关试题

