【题目】已知:如图,在△ABC中,∠A=90°,AB = AC,BD平分∠ABC。
求证:BC = AB + AD

参考答案:
【答案】证明见解析
【解析】试题分析: 过D作DE垂直于BC,由DA垂直于AB,且BD为角平分线,利用角平分线性质得出DA=DE,再由斜边BD为公共边,利用HL得出直角三角形ABD与直角三角形BED全等,由全等三角形的对应边相等得出AB=BE,由AB=AC,且BA与AC垂直得到三角形ABC为等腰直角三角形,可得出三角形DEC为等腰直角三角形,得出DE=EC,而BC=EB+EC,等量代换即可得证.
试题解析:
过D作DE⊥BC,交BC于点E,
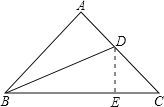
∵∠A=90,
∴DA⊥AB,
∵BD是∠ABC的平分线,DA⊥AB,DE⊥BC,
∴DA=DE,
在Rt△ABD和Rt△EBD中,
{BD=BDDA=DE,
∴Rt△ABD≌Rt△EBD(HL),
∴AB=BE,
又∵∠A=90,且AB=AC,
∴△ABC为等腰直角三角形,
∴∠C=∠ABC=45,又∠DEC=90,
∴△DEC为等腰直角三角形,
∴DE=EC,
∴AD=EC,
则BC=BE+EC=AB+AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
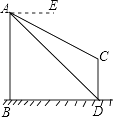
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号). -
科目: 来源: 题型:
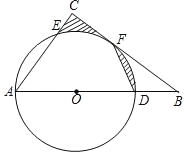
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知将二次函数y=x2+bx+c的图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣4x﹣5,则b= , c= .
-
科目: 来源: 题型:
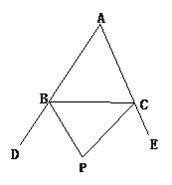
查看答案和解析>>【题目】如图,PB和PC是△ABC的两条外角平分线。
①求证:∠BPC=90°-
 ∠BAC.
∠BAC.②根据第①问的结论猜想:三角形的三条外角平分线所在的直线形成的三角形按角分类属于什么三角形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“同旁内角互补”中,题设是 , 结论是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在6×4的正方形网格中,点A、B、C、D、E、F都在格点上.连接点A、B得线段AB.
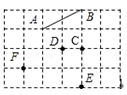
(1)连接C、D、E、F中的任意两点,共可得 条线段,在图中画出来;
(2)在(1)中所连得的线段中,与AB平行的线段是 ;
(3)用三角尺或量角器度量、检验,AB及(1)中所连得的线段中,互相垂直的线段有几对?(请用“⊥”表示出来) .
相关试题

