【题目】如图,直线![]() ∥
∥![]() ,⊙O与
,⊙O与![]() 和
和![]() 分别相切于点A和点B.直线MN与
分别相切于点A和点B.直线MN与![]() 相交于M,与
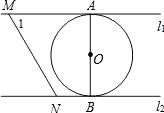
相交于M,与![]() 相交于N,⊙O的半径为1,∠1=60°,直线MN从如图所示位置向右平移,下列结论:①
相交于N,⊙O的半径为1,∠1=60°,直线MN从如图所示位置向右平移,下列结论:①![]() 和
和![]() 的距离为2;②MN=
的距离为2;②MN=![]() ;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=
;③当直线MN与⊙O相切时,∠MON=90°;④当AM+BN=![]() 时,直线MN与⊙O相切.其中正确的序号是 .
时,直线MN与⊙O相切.其中正确的序号是 .
参考答案:
【答案】①③④.
【解析】
试题分析:如图1,∵⊙O与![]() 和
和![]() 分别相切于点A和点B,∴OA⊥
分别相切于点A和点B,∴OA⊥![]() ,OB⊥
,OB⊥![]() ,∵
,∵![]() ∥
∥![]() ,∴点A、B、O共线,∴
,∴点A、B、O共线,∴![]() 和
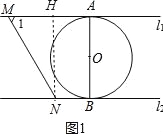
和![]() 的距离=AB=2,故①正确;作NH⊥AM,如图1,则四边形ABNH为矩形,∴NH=AB=2,在Rt△MNH中,∵∠1=60°,∴MH=
的距离=AB=2,故①正确;作NH⊥AM,如图1,则四边形ABNH为矩形,∴NH=AB=2,在Rt△MNH中,∵∠1=60°,∴MH=![]() NH=
NH=![]() ,∴MN=2MH=
,∴MN=2MH=![]() ,故②错误;当直线MN与⊙O相切时,如图2,∠1=∠2,∠3=∠4,∵
,故②错误;当直线MN与⊙O相切时,如图2,∠1=∠2,∠3=∠4,∵![]() ∥
∥![]() ,∴∠1+∠2+∠3+∠4=180°,∴∠1+∠3=90°,∴∠MON=90°,所以③正确;过点O作OC⊥MN于C,如图2,∵
,∴∠1+∠2+∠3+∠4=180°,∴∠1+∠3=90°,∴∠MON=90°,所以③正确;过点O作OC⊥MN于C,如图2,∵![]() ,∴
,∴![]() 1AM+
1AM+![]() 1BN+
1BN+![]() MNOC=
MNOC=![]() (BN+AM)2,即
(BN+AM)2,即![]() (AM+BN)+MNOC=AM+BN,∵AM+BN=
(AM+BN)+MNOC=AM+BN,∵AM+BN=![]() ,MN=
,MN=![]() ,∴OC=1,而OC⊥MN,∴直线MN与⊙O相切,所以④正确.
,∴OC=1,而OC⊥MN,∴直线MN与⊙O相切,所以④正确.
故答案为:①③④.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
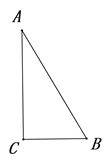
已知:如图,在
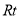 △
△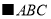 中,
中, 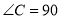 °,
°,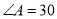 °.
°.求证:
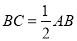 .
.证明:
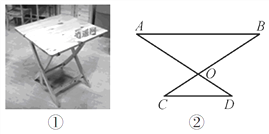
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得
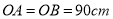 ,
, 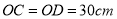 ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度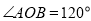 .
.求:桌面与地面的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一件衣服先按成本提高50%标价,再以8折(标价的80%)出售,结果获利28元,那么这件衣服的成本是元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 若AB=BC,则点B为线段AC的中点 B. 射线AB和射线BA是同一条射线
C. 两点之间的线段就是两点之间的距离 D. 同角的补角一定相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=﹣1时,代数式ax2+bx+1的值为﹣1,则(1+a﹣b)(1﹣a+b)的值为( )
A. ﹣3 B. ﹣1 C. 1 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
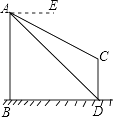
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号). -
科目: 来源: 题型:
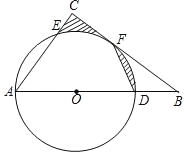
查看答案和解析>>【题目】在△ABC中,∠ACB=90°,O为边AB上的一点,以O为圆心,以OA为半径,作⊙O,交AB于点D,交AC于点E,交BC于点F,且点F恰好是ED的中点,连接DF.
(1)求证:BC是⊙O的切线;
(2)若⊙O的直径为10,AE=6,求图中阴影部分的面积.
相关试题

