【题目】感知:如图①,在平行四边形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() .过点
.过点![]() 的直线
的直线![]() 分别交边
分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .易证:
.易证:![]() (不需要证明).
(不需要证明).
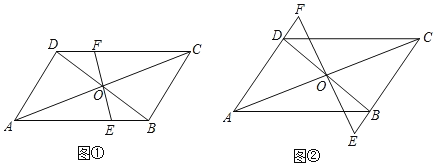
探究:若图①中的直线![]() 分别交边
分别交边![]() 、
、![]() 的延长线于点
的延长线于点![]() 、
、![]() ,其它条件不变,如图②.
,其它条件不变,如图②.
求证:![]() .
.
应用:在图②中,连结![]() .若
.若![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长是__________,四边形
的长是__________,四边形![]() 的面积是__________.
的面积是__________.
参考答案:
【答案】探究:证明见解析;应用:10,36
【解析】
探究:根据平行四边形的性质得到AB∥CD,OB=OD,根据AAS可证明△BOE≌△DOF.
应用:根据平行四边形的性质、梯形的面积公式计算即可.
探究:如图②.
∵四边形ABCD是平行四边形,∴AD∥BC,OD=OB,∴∠ODF=∠OBE,∠E=∠F.
在△BOE和△DOF中,∵ ,∴△BOE≌△DOF(AAS).
,∴△BOE≌△DOF(AAS).
应用:
∵∠ADB=90°,AB=10,AD=6,∴BD![]() 8.
8.
∵BE=![]() BC,BC=AD=6,∴BE=3.
BC,BC=AD=6,∴BE=3.
∵AD∥BE,∴BD⊥CE.在Rt△OBE中,OB![]() BD=4,BE=3,∴OE=5,由探究得:△BOE≌△DOF,∴OE=OF=5,∴EF=10,四边形AEBD的面积
BD=4,BE=3,∴OE=5,由探究得:△BOE≌△DOF,∴OE=OF=5,∴EF=10,四边形AEBD的面积![]() 36.
36.
故答案为:10,36.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(小时),两车之间的距离为
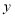 (千米),图中的折线表示
(千米),图中的折线表示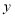 与
与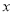 的函数关系.
的函数关系.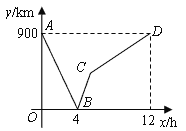
信息读取:
(1)甲、乙两地之间的距离为__________千米;
(2)请解释图中点
 的实际意义;
的实际意义;图像理解:
(3)求慢车和快车的速度;
(4)求线段
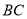 所示的
所示的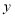 与
与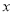 之间函数关系式.
之间函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在圆O中,AO、BO是圆O的半径,点C在劣弧
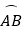 上,
上,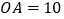 ,
,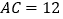 ,
,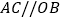 ,联结AB.
,联结AB. 如图1,求证:AB平分
如图1,求证:AB平分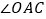 ;
; 点M在弦AC的延长线上,联结BM,如果
点M在弦AC的延长线上,联结BM,如果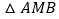 是直角三角形,请你在如图2中画出点M的位置并求CM的长;
是直角三角形,请你在如图2中画出点M的位置并求CM的长; 如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,
如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,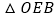 的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.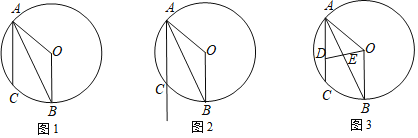
-
科目: 来源: 题型:
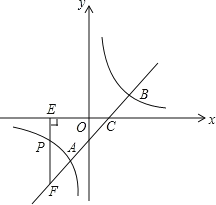
查看答案和解析>>【题目】如图,直线
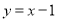 与反比例函数
与反比例函数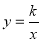 的图象交于
的图象交于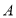 、
、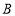 两点,与
两点,与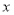 轴交于点
轴交于点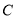 ,已知点
,已知点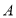 的坐标为
的坐标为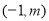 .
.
(1)求反比例函数的解析式;
(2)若点
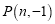 是反比例函数图象上一点,过点
是反比例函数图象上一点,过点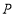 作
作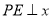 轴于点
轴于点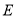 ,延长
,延长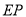 交直线
交直线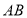 于点
于点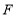 ,求
,求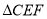 的面积.
的面积. -
科目: 来源: 题型:
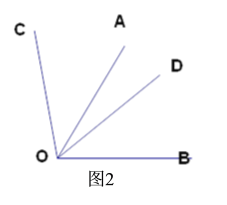
查看答案和解析>>【题目】(1)如图 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代数式表示∠BOC.

(2)如图2,若∠AOB=∠COD=60°,直接写出∠AOC与∠BOD的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
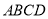 的对角线相交于点
的对角线相交于点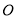 ,
,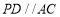 ,
,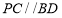 .
.
(1)求证:四边形
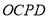 是菱形;
是菱形;(2)若将题设中“矩形
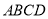 ”这一条件改为“菱形
”这一条件改为“菱形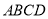 ”,其余条件不变,则四边形
”,其余条件不变,则四边形 是__________形.
是__________形.
相关试题

