【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(小时),两车之间的距离为![]() (千米),图中的折线表示
(千米),图中的折线表示![]() 与
与![]() 的函数关系.
的函数关系.
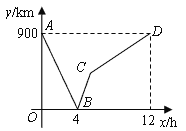
信息读取:
(1)甲、乙两地之间的距离为__________千米;
(2)请解释图中点![]() 的实际意义;
的实际意义;
图像理解:
(3)求慢车和快车的速度;
(4)求线段![]() 所示的
所示的![]() 与
与![]() 之间函数关系式.
之间函数关系式.
参考答案:
【答案】(1)900;(2)当两车出发4小时时相遇;(3)慢车的速度是75千米/时,快车的速度是150千米/时;(4)y=225x﹣900(4≤x≤6).
【解析】
(1)根据已知条件和函数图象可以直接写出甲、乙两地之间的距离;
(2)根据题意可以得到点B表示的实际意义;
(3)根据图象和题意可以分别求出慢车和快车的速度;
(4)根据题意可以求得点C的坐标,由图象可以得到点B的坐标,从而可以得到线段BC所表示的y与x之间的函数关系式,以及自变量x的取值范围.
(1)由图象可得:甲、乙两地之间的距离为900千米.
故答案为:900;
(2)图中点B的实际意义时当两车出发4小时时相遇;
(3)由题意可得:慢车的速度为:900÷12=75,快车的速度为:(900﹣75×4)÷4=150,即慢车的速度是75千米/时,快车的速度是150千米/时;
(4)由题可得:点C是快车刚到达乙地,∴点C的横坐标是:900÷150=6,纵坐标是:900﹣75×6=450,即点C的坐标为(6,450),设线段BC对应的函数解析式为y=kx+b.
∵点B(4,0),点C(6,450),∴![]() ,得:
,得:![]() ,即线段BC所表示的y与x之间的函数关系式是y=225x﹣900(4≤x≤6).
,即线段BC所表示的y与x之间的函数关系式是y=225x﹣900(4≤x≤6).
-
科目: 来源: 题型:
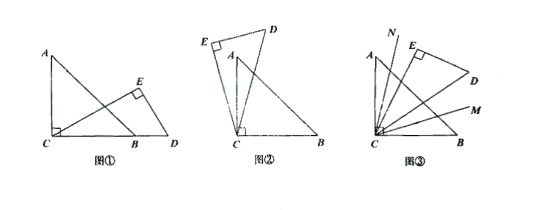
查看答案和解析>>【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,正方形
 的边长为4厘米,点
的边长为4厘米,点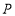 从点
从点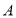 出发,经
出发,经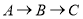 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点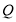 从点
从点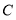 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿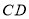 向点
向点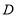 运动,设运动时间为t秒,
运动,设运动时间为t秒,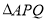 的面积为
的面积为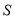 平方厘米.
平方厘米.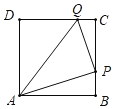
(1)当
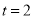 时,
时,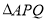 的面积为__________平方厘米;
的面积为__________平方厘米;(2)求
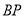 的长(用含
的长(用含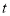 的代数式表示);
的代数式表示);(3)当点
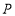 在线段
在线段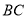 上运动,且
上运动,且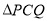 为等腰三角形时,求此时
为等腰三角形时,求此时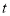 的值;
的值;(4)求
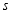 与
与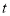 之间的函数关系式.
之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在圆O中,AO、BO是圆O的半径,点C在劣弧
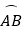 上,
上,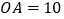 ,
,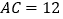 ,
,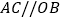 ,联结AB.
,联结AB.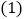 如图1,求证:AB平分
如图1,求证:AB平分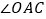 ;
; 点M在弦AC的延长线上,联结BM,如果
点M在弦AC的延长线上,联结BM,如果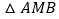 是直角三角形,请你在如图2中画出点M的位置并求CM的长;
是直角三角形,请你在如图2中画出点M的位置并求CM的长;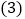 如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,
如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x, 的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.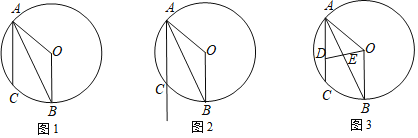
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,在平行四边形
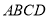 中,对角线
中,对角线 、
、 交于点
交于点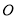 .过点
.过点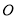 的直线
的直线 分别交边
分别交边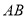 、
、 于点
于点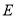 、
、 .易证:
.易证: (不需要证明).
(不需要证明).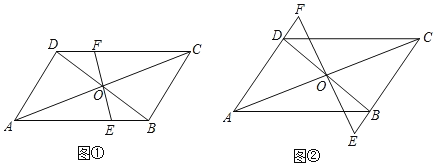
探究:若图①中的直线
 分别交边
分别交边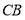 、
、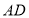 的延长线于点
的延长线于点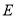 、
、 ,其它条件不变,如图②.
,其它条件不变,如图②.求证:
 .
.应用:在图②中,连结
 .若
.若 ,
, ,
,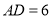 ,
, ,则
,则 的长是__________,四边形
的长是__________,四边形 的面积是__________.
的面积是__________. -
科目: 来源: 题型:
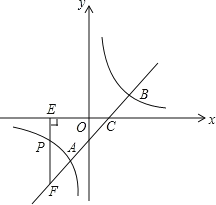
查看答案和解析>>【题目】如图,直线
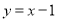 与反比例函数
与反比例函数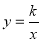 的图象交于
的图象交于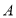 、
、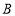 两点,与
两点,与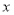 轴交于点
轴交于点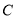 ,已知点
,已知点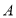 的坐标为
的坐标为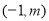 .
.
(1)求反比例函数的解析式;
(2)若点
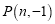 是反比例函数图象上一点,过点
是反比例函数图象上一点,过点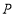 作
作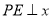 轴于点
轴于点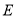 ,延长
,延长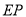 交直线
交直线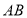 于点
于点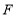 ,求
,求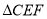 的面积.
的面积.
相关试题

