【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了 名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
参考答案:
【答案】(1)100,108°;(2)详见解析;(3)600.
【解析】试题分析:(1)先利用QQ计算出宗人数,再用百分比计算度数.
(2)按照扇形图补充条形图.(3)利用微信沟通所占百分比计算总人数.
试题解析:(1)喜欢用电话沟通的人数为20,所占百分比为20%,
∴此次共抽查了:20÷20%=100人.
喜欢用QQ沟通所占比例为: ![]() ,
,
∴QQ的扇形圆心角的度数为:360°×![]() =108°.
=108°.
(2)喜欢用短信的人数为:100×5%=5人
喜欢用微信的人数为:100﹣20﹣5﹣30﹣5=40.
补充图形(略)
(3)喜欢用微信沟通所占百分比为: ![]() ×100%=40%.
×100%=40%.
∴该校共有1500名学生,估计该校最喜欢用“微信”进行沟通的学生有:1500×40%=600人 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
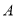 在反比例函数,
在反比例函数,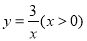 的图像上,点
的图像上,点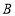 在反比例函数
在反比例函数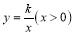 的图像上,
的图像上,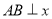 轴于点
轴于点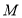 .且
.且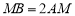 ,则
,则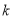 的值为( )
的值为( )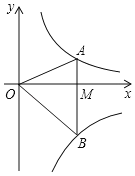
A.-3B.-6C.2D.6
-
科目: 来源: 题型:
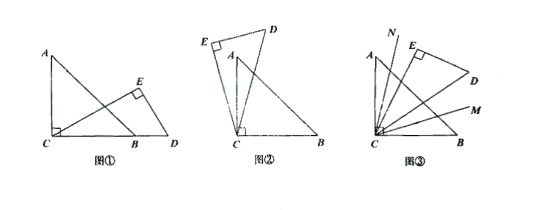
查看答案和解析>>【题目】如图,将一个直角三角板中30°的锐角顶点与另一个直角三角板的直角顶点叠放一起.(注:∠ACB与∠DEC是直角,∠A=45°,∠DEC=30°).
(1)如图①,若点C、B、D在一条直线上,求∠ACE的度数;
(2)如图②,将直角三角板CDE绕点c逆时针方向转动到某个位置,若恰好平分∠DCE,求∠BCD的度数;
(3)如图③若∠DEC始终在∠ACB的内部,分别作射线CM平分∠BCD,射线CN平分∠ACE.如果三角板DCE在∠ACB内绕点C任意转动,∠MCN的度数是否发生变化?如果不变,求出它的度数,如果变化,说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,正方形
 的边长为4厘米,点
的边长为4厘米,点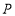 从点
从点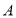 出发,经
出发,经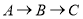 沿正方形的边以2厘米/秒的速度运动;同时,点
沿正方形的边以2厘米/秒的速度运动;同时,点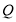 从点
从点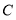 出发以1厘米/秒的速度沿
出发以1厘米/秒的速度沿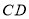 向点
向点 运动,设运动时间为t秒,
运动,设运动时间为t秒,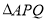 的面积为
的面积为 平方厘米.
平方厘米.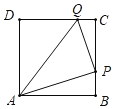
(1)当
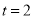 时,
时,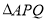 的面积为__________平方厘米;
的面积为__________平方厘米;(2)求
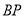 的长(用含
的长(用含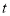 的代数式表示);
的代数式表示);(3)当点
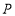 在线段
在线段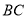 上运动,且
上运动,且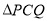 为等腰三角形时,求此时
为等腰三角形时,求此时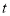 的值;
的值;(4)求
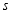 与
与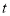 之间的函数关系式.
之间的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(小时),两车之间的距离为
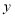 (千米),图中的折线表示
(千米),图中的折线表示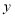 与
与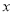 的函数关系.
的函数关系.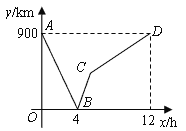
信息读取:
(1)甲、乙两地之间的距离为__________千米;
(2)请解释图中点
 的实际意义;
的实际意义;图像理解:
(3)求慢车和快车的速度;
(4)求线段
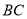 所示的
所示的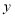 与
与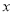 之间函数关系式.
之间函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在圆O中,AO、BO是圆O的半径,点C在劣弧
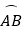 上,
上,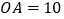 ,
,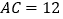 ,
,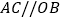 ,联结AB.
,联结AB.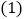 如图1,求证:AB平分
如图1,求证:AB平分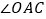 ;
;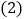 点M在弦AC的延长线上,联结BM,如果
点M在弦AC的延长线上,联结BM,如果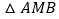 是直角三角形,请你在如图2中画出点M的位置并求CM的长;
是直角三角形,请你在如图2中画出点M的位置并求CM的长;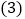 如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,
如图3,点D在弦AC上,与点A不重合,联结OD与弦AB交于点E,设点D与点C的距离为x,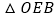 的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.
的面积为y,求y与x的函数关系式,并写出自变量x的取值范围.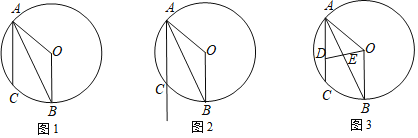
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,在平行四边形
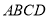 中,对角线
中,对角线 、
、 交于点
交于点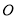 .过点
.过点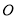 的直线
的直线 分别交边
分别交边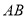 、
、 于点
于点 、
、 .易证:
.易证: (不需要证明).
(不需要证明).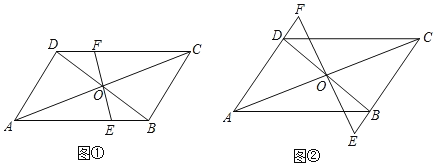
探究:若图①中的直线
 分别交边
分别交边 、
、 的延长线于点
的延长线于点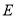 、
、 ,其它条件不变,如图②.
,其它条件不变,如图②.求证:
 .
.应用:在图②中,连结
 .若
.若 ,
, ,
,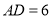 ,
, ,则
,则 的长是__________,四边形
的长是__________,四边形 的面积是__________.
的面积是__________.
相关试题

