【题目】如图,矩形![]() 的对角线相交于点
的对角线相交于点![]() ,
,![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若将题设中“矩形![]() ”这一条件改为“菱形
”这一条件改为“菱形![]() ”,其余条件不变,则四边形
”,其余条件不变,则四边形![]() 是__________形.
是__________形.
参考答案:
【答案】(1)证明见解析;(2)矩.
【解析】
(1)由PD∥AC,PC∥BD,易得四边形OCPD是平行四边形,又由矩形ABCD的对角线互相平分且相等,即可得OC=OD,继而证得四边形OCPD是菱形;
(2)由PD∥AC,PC∥BD,易得四边形OCPD是平行四边形,又由菱形的对角线互相垂直,即可得AC⊥BD,继而证得四边形OCPD是矩形.
(1)∵PD∥AC,PC∥BD,∴四边形OCPD是平行四边形.
∵四边形ABCD是矩形,∴AC=BD,OD![]() BD,OC
BD,OC![]() AC,∴OC=OD,∴四边形OCPD是菱形;
AC,∴OC=OD,∴四边形OCPD是菱形;
(2)矩形.证明如下:
∵PD∥AC,PC∥BD,∴四边形OCPD是平行四边形.
∵四边形ABCD是菱形,∴AC⊥BD,∴∠COD=90°,∴四边形OCPD是矩形.
故答案为:矩.
-
科目: 来源: 题型:
查看答案和解析>>【题目】感知:如图①,在平行四边形
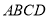 中,对角线
中,对角线 、
、 交于点
交于点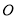 .过点
.过点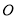 的直线
的直线 分别交边
分别交边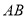 、
、 于点
于点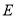 、
、 .易证:
.易证: (不需要证明).
(不需要证明).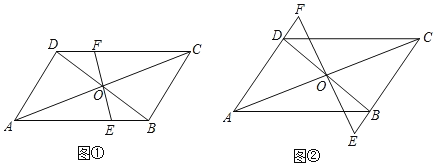
探究:若图①中的直线
 分别交边
分别交边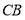 、
、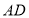 的延长线于点
的延长线于点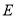 、
、 ,其它条件不变,如图②.
,其它条件不变,如图②.求证:
 .
.应用:在图②中,连结
 .若
.若 ,
, ,
,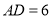 ,
, ,则
,则 的长是__________,四边形
的长是__________,四边形 的面积是__________.
的面积是__________. -
科目: 来源: 题型:
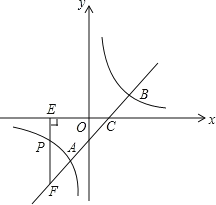
查看答案和解析>>【题目】如图,直线
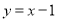 与反比例函数
与反比例函数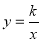 的图象交于
的图象交于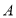 、
、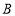 两点,与
两点,与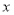 轴交于点
轴交于点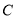 ,已知点
,已知点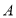 的坐标为
的坐标为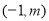 .
.
(1)求反比例函数的解析式;
(2)若点
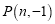 是反比例函数图象上一点,过点
是反比例函数图象上一点,过点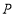 作
作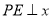 轴于点
轴于点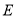 ,延长
,延长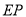 交直线
交直线 于点
于点 ,求
,求 的面积.
的面积. -
科目: 来源: 题型:
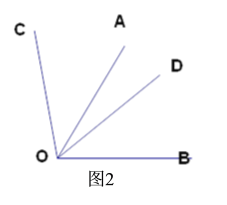
查看答案和解析>>【题目】(1)如图 ,∠AOB=∠COD=90°
①∠AOD=30°求∠BOC
②若∠AOD=α求用α的代数式表示∠BOC.

(2)如图2,若∠AOB=∠COD=60°,直接写出∠AOC与∠BOD的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为提高学生的汉字书写能力,开展了“汉字听写”大赛.七、八年级各有150人参加比赛,为了解这两个年级参加比赛学生的成绩情况,从中各随机抽取10名学生的成绩,数据如下:
七年级 88 94 90 94 84 94 99 94 99 100
八年级 84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:

分析数据:补全下列表格中的统计量:

得出结论:你认为抽取的学生哪个年级的成绩较为稳定?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,则下列结论:①△ABF≌△CAE;②∠AHC=120°;③△AEH∽△CEA;④AEAD=AHAF;其中结论正确的个数是( )
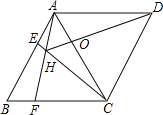
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年3月21日,长春市遭遇了一次大量降雪天气,市环保系统出动了多辆清雪车连夜清雪,已知一台大型清雪车比一台小型清雪车每小时多清扫路面6千米,一台大型清雪车清扫路面90千米与一台小型清雪车清扫路面60千米所用的时间相同.求一台小型清雪车每小时清扫路面的长度.
相关试题

