【题目】如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4,则BN的长为__________;
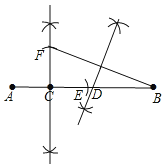
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,不写画法,保留作图痕迹,画出一种情形即可)
![]()

参考答案:
【答案】![]() 或5
或5
【解析】分析:(1)①当MN为最大线段时,由勾股定理求出BN;②当BN为最大线段时,由勾股定理求出BN即可;
(2)①在AB上截取CE=CA;②作AE的垂直平分线,并截取CF=CA;③连接BF,并作BF的垂直平分线,交AB于D.
详解:(1)①当MN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BM=![]() ,
,
②当BN为最大线段时,
∵点M,N是线段AB的勾股分割点,
∴BN=![]() ,
,
综上,BN=![]() 或5;
或5;
(2)作法:①在AB上截取CE=CA;
②作AE的垂直平分线,并截取CF=CA;
③连接BF,并作BF的垂直平分线,交AB于D;
点D即为所求;如图所示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
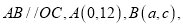
 ,并且
,并且 满足
满足 .一动点
.一动点 从点
从点 出发,在线段
出发,在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 移动;动点
移动;动点 从点
从点 出发在线段
出发在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 运动,点
运动,点 分别从点
分别从点 同时出发,当点
同时出发,当点 运动到点
运动到点 时,点
时,点 随之停止运动.设运动时间为
随之停止运动.设运动时间为 (秒)
(秒)
(1)求
 两点的坐标;
两点的坐标;(2)当
 为何值时,四边形
为何值时,四边形 是平行四边形?并求出此时
是平行四边形?并求出此时 两点的坐标.
两点的坐标.(3)当
 为何值时,
为何值时, 是以
是以 为腰的等腰三角形?并求出此时
为腰的等腰三角形?并求出此时 两点的坐标.
两点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
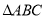 中,
中,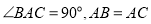 ,点
,点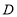 为直线
为直线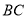 上一动点(点
上一动点(点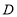 不与
不与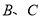 重合).以
重合).以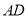 为边作正方形
为边作正方形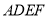 ,连接
,连接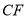 .
.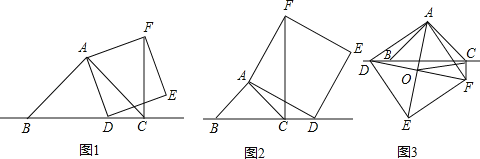
(1)如图1,当点
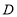 在线段
在线段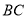 上时,求证:
上时,求证: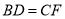 .
.(2)如图2,当点
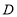 在线段
在线段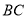 的延长线上时,其他条件不变,请直接写出
的延长线上时,其他条件不变,请直接写出 三条线段之间的关系;
三条线段之间的关系;(3)如图3,当点
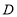 在线段
在线段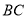 的反向延长线上时,且点
的反向延长线上时,且点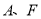 分别在直线
分别在直线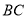 的两侧.其他条件不变,若连接正方形对角线
的两侧.其他条件不变,若连接正方形对角线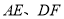 ,交点为
,交点为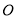 ,连接
,连接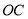 ,探究
,探究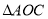 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是射线
是射线 上一点,过
上一点,过 作
作 轴于点
轴于点 ,以
,以 为边在其右侧作正方形
为边在其右侧作正方形 ,过
,过 的双曲线
的双曲线 交
交 边于点
边于点 ,则
,则 的值为
的值为


A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
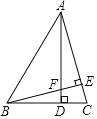
查看答案和解析>>【题目】如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且 .将
.将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 .连结
.连结 、
、 .下列结论:①
.下列结论:① ;②
;② ;③
;③ 是正三角形;④
是正三角形;④ 的面积为90.其中正确的是______(填所有正确答案的序号).
的面积为90.其中正确的是______(填所有正确答案的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
理解:(1)如图
 ,已知
,已知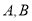 是⊙
是⊙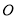 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点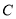 ,使
,使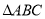 为“智慧三角形”(画出点
为“智慧三角形”(画出点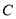 的位置,保留作图痕迹);
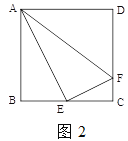
的位置,保留作图痕迹);(2)如图
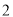 ,在正方形
,在正方形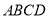 中,
中, 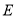 是
是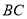 的中点,
的中点, 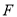 是
是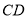 上一点,且
上一点,且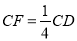 ,试判断
,试判断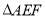 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;运用:(3)如图
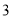 ,在平面直角坐标系
,在平面直角坐标系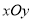 中,⊙
中,⊙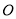 的半径为
的半径为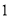 ,点
,点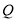 是直线
是直线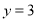 上的一点,若在⊙
上的一点,若在⊙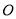 上存在一点
上存在一点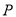 ,使得
,使得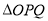 为“智慧三角形”,其面积的最小值为______.
为“智慧三角形”,其面积的最小值为______.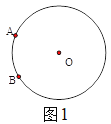
相关试题

