【题目】如图,在平面直角坐标系中,![]()
![]() ,并且
,并且![]() 满足
满足![]() .一动点
.一动点![]() 从点
从点![]() 出发,在线段
出发,在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动;动点
移动;动点![]() 从点
从点![]() 出发在线段
出发在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 运动,点
运动,点![]() 分别从点
分别从点![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,点
时,点![]() 随之停止运动.设运动时间为
随之停止运动.设运动时间为![]() (秒)
(秒)

(1)求![]() 两点的坐标;
两点的坐标;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形?并求出此时
是平行四边形?并求出此时![]() 两点的坐标.
两点的坐标.
(3)当![]() 为何值时,
为何值时,![]() 是以
是以![]() 为腰的等腰三角形?并求出此时
为腰的等腰三角形?并求出此时![]() 两点的坐标.
两点的坐标.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】
(1)由二次根式有意义的条件可求出a、b的值,再根据已知即可求得答案;
(2)由题意得:![]() ,则
,则![]() ,当
,当![]() 时,四边形
时,四边形![]() 是平行四边形,由此可得关于t的方程,求出t的值即可求得答案;
是平行四边形,由此可得关于t的方程,求出t的值即可求得答案;
(3)分![]() 、
、![]() 两种情况分别画出符合题意的图形,
两种情况分别画出符合题意的图形,
(1)由![]() ,
,
则![]() ,
,
![]() ,
,
∵AB//OC,A(0,12),B(a,c),
∴c=12,
∴![]() ;
;
(2)如图,
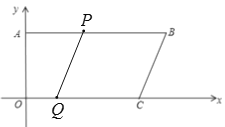
由题意得:![]() ,
,
则:![]() ,
,
![]() 当
当![]() 时,四边形
时,四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
解得:![]() ,
,
![]() ;
;
(3)当![]() 时,过
时,过![]() 作
作![]() ,则四边形AOQN是矩形,
,则四边形AOQN是矩形,
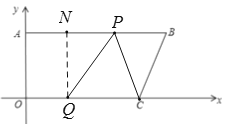
∴AN=OQ=t,QN=OA=12,
∴PN=t,
由题意得:![]() ,
,
解得:![]() ,
,
故![]() ,
,
当![]() 时,过
时,过![]() 作
作![]() 轴,
轴,

由题意得:![]() ,
,
则![]() ,
,
解得:![]() ,
,
故![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶(500ml)、红茶(500ml)和可乐(600ml),抽奖规则如下:①如图,是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字和奖品名称的两个字相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:
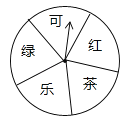
(1)求一次“有效随机转动”可获得“乐”字的概率;
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或树状图等方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
-
科目: 来源: 题型:
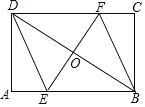
查看答案和解析>>【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐30千克为标准,超过千克数记作正数,不足的千克数记作负数,称后的记录如下表:
与标准质量的差值(单位:千克)
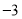
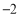
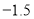
0
1
2.5
筐数
1
4
4
2
3
6
(1)20筐白菜中,最重的一筐比最轻的一筐重 千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价3.5元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在
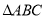 中,
中,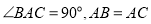 ,点
,点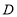 为直线
为直线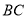 上一动点(点
上一动点(点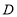 不与
不与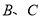 重合).以
重合).以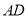 为边作正方形
为边作正方形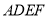 ,连接
,连接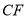 .
.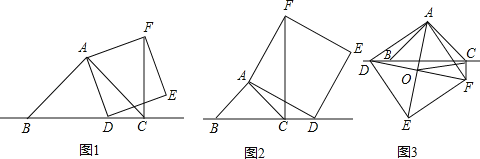
(1)如图1,当点
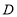 在线段
在线段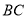 上时,求证:
上时,求证: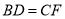 .
.(2)如图2,当点
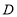 在线段
在线段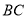 的延长线上时,其他条件不变,请直接写出
的延长线上时,其他条件不变,请直接写出 三条线段之间的关系;
三条线段之间的关系;(3)如图3,当点
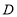 在线段
在线段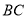 的反向延长线上时,且点
的反向延长线上时,且点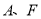 分别在直线
分别在直线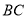 的两侧.其他条件不变,若连接正方形对角线
的两侧.其他条件不变,若连接正方形对角线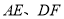 ,交点为
,交点为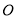 ,连接
,连接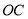 ,探究
,探究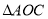 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是射线
是射线 上一点,过
上一点,过 作
作 轴于点
轴于点 ,以
,以 为边在其右侧作正方形
为边在其右侧作正方形 ,过
,过 的双曲线
的双曲线 交
交 边于点
边于点 ,则
,则 的值为
的值为


A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4,则BN的长为__________;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,不写画法,保留作图痕迹,画出一种情形即可)


相关试题

