【题目】定义:数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.
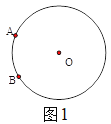
理解:(1)如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
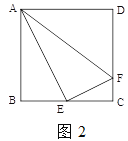
(2)如图![]() ,在正方形
,在正方形![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
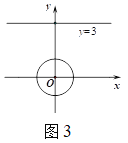
运用:(3)如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,其面积的最小值为______.
为“智慧三角形”,其面积的最小值为______.
参考答案:
【答案】![]()
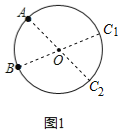
【解析】分析:(1)连结AO并且延长交圆于C1,连结BO并且延长交圆于C2,即可求解;
(2)设正方形的边长为4a,表示出DF、CF以及EC、BE的长,然后根据勾股定理列式表示出AF2、EF2、AE2,再根据勾股定理逆定理判定△AEF是直角三角形,由直角三角形的性质可得△AEF为“智慧三角形”;
(3)根据“智慧三角形”的定义可得△OPQ为直角三角形,根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,由垂线段最短可得斜边最短为3,根据勾股定理可求另一条直角边,再根据三角形面积可求斜边的高,即点P的横坐标,再根据勾股定理可求点P的纵坐标,从而求解.
详解:(1)如图1所示:
(2)△AEF是否为“智慧三角形”,
理由如下:设正方形的边长为4a,
∵E是DC的中点,
∴DE=CE=2a,
∵BC:FC=4:1,
∴FC=a,BF=4a﹣a=3a,
在Rt△ADE中,AE2=(4a)2+(2a)2=20a2,
在Rt△ECF中,EF2=(2a)2+a2=5a2,
在Rt△ABF中,AF2=(4a)2+(3a)2=25a2,
∴AE2+EF2=AF2,
∴△AEF是直角三角形,
∵斜边AF上的中线等于AF的一半,
∴△AEF为“智慧三角形”;
(3)如图3所示:
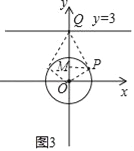
由“智慧三角形”的定义可得△OPQ为直角三角形,
根据题意可得一条直角边为1,当斜边最短时,另一条直角边最短,则面积取得最小值,
由垂线段最短可得斜边最短为3,
由勾股定理可得PQ=![]() ,
,
PM=1×2![]() ÷3=
÷3=![]() ,
,
面积的最小值为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=3,MN=4,则BN的长为__________;
(2)已知点C是线段AB上的一定点,其位置如图2所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,不写画法,保留作图痕迹,画出一种情形即可)


-
科目: 来源: 题型:
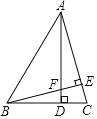
查看答案和解析>>【题目】如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,则△ABC的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,点
,点 在边
在边 上,且
上,且 .将
.将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 .连结
.连结 、
、 .下列结论:①
.下列结论:① ;②
;② ;③
;③ 是正三角形;④
是正三角形;④ 的面积为90.其中正确的是______(填所有正确答案的序号).
的面积为90.其中正确的是______(填所有正确答案的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校有3000名学生.为了解全校学生的上学方式,该校数学兴趣小组以问卷调查的形式,随机调查了该校部分学生的主要上学方式(参与问卷调查的学生只能从以下六个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类
A
B
C
D
E
F
上学方式
电动车
私家车
公共交通
自行车
步行
其他
某校部分学生主要上学方式扇形统计图某校部分学生主要上学方式条形统计图

根据以上信息,回答下列问题:
(1)参与本次问卷调查的学生共有____人,其中选择B类的人数有____人.
(2)在扇形统计图中,求E类对应的扇形圆心角α的度数,并补全条形统计图.
(3)若将A、C、D、E这四类上学方式视为“绿色出行”,请估计该校每天“绿色出行”的学生人数.
-
科目: 来源: 题型:
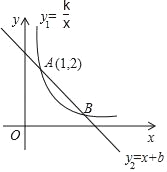
查看答案和解析>>【题目】反比例函数y1=
 (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有
 两种型号的健身器可供选择.
两种型号的健身器可供选择.(1)劲松公司2015年每套
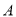 型健身器的售价为
型健身器的售价为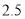 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为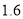 万元,求每套
万元,求每套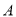 型健身器年平均下降率
型健身器年平均下降率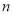 ;
;(2)2017年市政府经过招标,决定年内采购并安装劲松公司
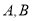 两种型号的健身器材共
两种型号的健身器材共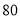 套,采购专项费总计不超过
套,采购专项费总计不超过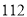 万元,采购合同规定:每套
万元,采购合同规定:每套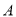 型健身器售价为
型健身器售价为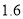 万元,每套
万元,每套 型健身器售价我
型健身器售价我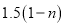 万元.
万元.①
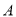 型健身器最多可购买多少套?
型健身器最多可购买多少套? ②安装完成后,若每套
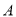 型和
型和 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的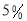 和
和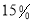 .市政府计划支出
.市政府计划支出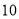 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
相关试题

