【题目】已知三角形的一锐角α(45°<α<90°)的正弦和余弦分别是方程(m+5)x2﹣(2m﹣5)x+12=0的两根,求:
(1)m的值;
(2)α的正弦值和余弦值.
参考答案:
【答案】(1)20;(2)sinα=![]() ,cosα=
,cosα=![]()
【解析】
(1)设一个直角三角形的两个锐角为∠A、∠B,且∠A+∠B=90°,利用正弦三角公式及完全平方公式得![]() ﹣2sinAsinB=1,列一元二次方程求解即可;
﹣2sinAsinB=1,列一元二次方程求解即可;
(2) 当m=20时,方程转化为(5x﹣3)(5x﹣4)=0,求解即可得到正弦值和余弦值,且注意α为锐角.
解:(1)设一个直角三角形的两个锐角为∠A、∠B(∠A+∠B=90°),
∴sinB=cosA,
根据题意,得:sinA+sinB=![]() ,sinAsinB=
,sinAsinB=![]() ,
,
∵![]() ,
,
∴![]() ﹣2sinAsinB=1,
﹣2sinAsinB=1,
∴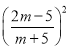 ﹣2×
﹣2×![]() =1,
=1,
解得![]() =20,
=20,![]() =﹣2,
=﹣2,
检验:把![]() =20代入检验是原方程的根,把
=20代入检验是原方程的根,把![]() =﹣2代入检验是原方程的根,
=﹣2代入检验是原方程的根,
∵sinA+sinB=![]() >0,sinAsinB=
>0,sinAsinB=![]() <1,
<1,
∴m=20;
(2)当m=20时,方程转化为(5x﹣3)(5x﹣4)=0,
解得![]() ,
,
∵45°<α<90°,
∴sinα>cosα,
∴sinα=![]() ,cosα=
,cosα=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
 的图象经过点(
的图象经过点(  ,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).
,8),直线y=﹣x+b经过该反比例函数图象上的点Q(4,m).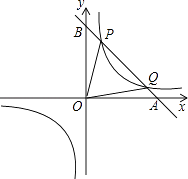
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x轴、y轴分别相交于A、B两点,与反比例函数图象的另一个交点为P,连接0P、OQ,求△OPQ的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC.

(1)尺规作图:作∠BAC的角平分线AD,交BC于点D.(不要求写作法,保留作图痕迹)
(2)延长AD至E点,使DE=AD,连接BE、CE.求证:四边形ABEC是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).

(1)求抛物线的解析式.
(2)D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连结BD、CD设点D的横坐标为m,△BCD的面积为S.
①求S关于m的函数关系式及自变量m的取值范围.
②当m为何值时,S有最大值,并求这个最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
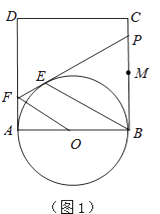
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )

A.2:5
B.2:3
C.3:5
D.3:2
相关试题

