Question

【题目】如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．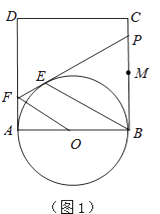

（1）求证：OF∥BE；
（2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；
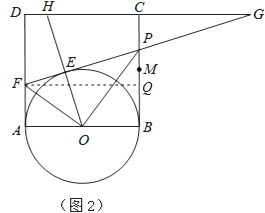
（3）延长DC、FP交于点G，连接OE并延长交直线DC于H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．

Answer 1

【答案】
（1）证明：连接OE

FE、FA是⊙O的两条切线

∴∠FAO=∠FEO=90°

在Rt△OAF和Rt△OEF中，

∴Rt△FAO≌Rt△FEO（HL），

∴∠AOF=∠EOF= ∠AOE，

∴∠AOF=∠ABE，

∴OF∥BE，

（2）解：过F作FQ⊥BC于Q

∴PQ=BP﹣BQ=x﹣y

PF=EF+EP=FA+BP=x+y

∵在Rt△PFQ中

∴FQ2+QP2=PF2

∴22+（x﹣y）2=（x+y）2

化简得： ，（1＜x＜2）

（3）解：存在这样的P点，

理由：∵∠EOF=∠AOF，

∴∠EHG=∠EOA=2∠EOF，

当∠EFO=∠EHG=2∠EOF时，

即∠EOF=30°时，Rt△EFO∽Rt△EHG，

此时Rt△AFO中，

y=AF=OAtan30°= ，

∴

∴当 时，△EFO∽△EHG

【解析】（1）根据正方形和切线的性质得到Rt△FAO≌Rt△FEO，得到∠AOF=∠ABE，根据平行线的判定方法得到OF∥BE；（2）根据切线性质得到PF=EF+EP=FA+BP，根据勾股定理求出BP，AF的关系；（3）根据正方形的性质和相似三角形的判定得到Rt△EFO∽Rt△EHG，根据直角三角形中特殊角的函数值求出x、y的值，得到△EFO∽△EHG.