【题目】如图,在ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
A.2:5
B.2:3
C.3:5
D.3:2
参考答案:
【答案】B
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∵S△DEF:S△ABF=4:25,
∴DE:AB=2:5,
∵AB=CD,
∴DE:EC=2:3.
所以答案是:B.
【考点精析】掌握平行四边形的性质和相似三角形的判定与性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的一锐角α(45°<α<90°)的正弦和余弦分别是方程(m+5)x2﹣(2m﹣5)x+12=0的两根,求:
(1)m的值;
(2)α的正弦值和余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不与M、C重合),以AB为直径作⊙O,过点P作⊙O的切线,交AD于点F,切点为E.
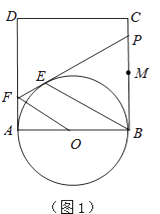
(1)求证:OF∥BE;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC、FP交于点G,连接OE并延长交直线DC于H(图2),问是否存在点P,使△EFO∽△EHG(E、F、O与E、H、G为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,关于x的二次函数y=x2﹣x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a﹣1)x+m的图象可能是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )

A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点
 .
.(1)点M到y轴的距离为1时,M的坐标?
(2)点
 且MN//x轴时,M的坐标?
且MN//x轴时,M的坐标? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.
B.
C.
D.
相关试题

