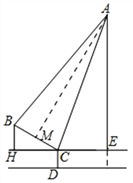
【题目】如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为1.8米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米,参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)

参考答案:
【答案】点A到地面的距离为12.9米.
【解析】试题分析:过点A作AM⊥BC于M,先证明∠ABC=∠ACB,推出AB=AC.在Rt△ACM中,求出AC,再在Rt△ACE中求出AE即可解决问题.
试题解析:解:由题可知,BH⊥HE,AE⊥HE,CD=2米,BC=4米,∠BCH=30°,∠ABC=80°,∠ACE=70°.∵∠BCH+∠ACB+∠ACE=180°,∴∠ACB=80°.
∵∠ABC=80°,∴∠ABC=∠ACB,∴AB=AC.
过点A作AM⊥BC于M,则CM=BM=2米.
∵在Rt△ACM中,CM=2米,∠ACB=80°,∴![]() =cos∠ACB=cos80°≈0.17,∴AC=
=cos∠ACB=cos80°≈0.17,∴AC=![]() =
=![]() (米).∵在Rt△ACE中,AC=
(米).∵在Rt△ACE中,AC=![]() ,∠ACE=70°,∴
,∠ACE=70°,∴![]() =sin∠ACE=sin70°≈0.94,
=sin∠ACE=sin70°≈0.94,
∴AE=![]() ×0.94=
×0.94=![]() ≈11.1(米),11.1+2=13.1(米)
≈11.1(米),11.1+2=13.1(米)
故点A到地面的高度为13.1米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,∠BOC=20°,OE平分∠AOC,则∠AOE=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟)
0
10
…
25
水池的容积V(公升)
100
300
…
600
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=80°.
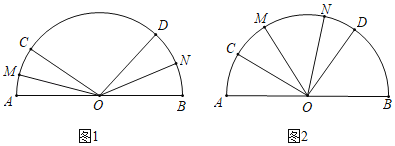
(1)如图1,OM平分∠AOC,ON平分∠BOD,求∠MON的度数;
(2)如图2,若∠AOC=x°,OM平分∠AOD,ON平分∠BOC,求∠MON的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.

-
科目: 来源: 题型:
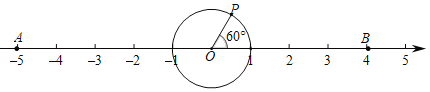
查看答案和解析>>【题目】点A和B在数轴上对应的数分别为a和b,且(a+5)2+|b﹣4|=0.
(1)求线段AB的长;
(2)点C在数轴上所对应的数为x,且x是方程x﹣3=
 x﹣1的解,在线段BC上是否存在点D,使得AD+BD=
x﹣1的解,在线段BC上是否存在点D,使得AD+BD=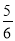 CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;(3)如图,PO=1,点P在AB的上方,且∠POB=60°,点P绕着点O以30度/秒的速度在圆周上顺时针旋转一周停止,同时点Q沿线段AB自点A向点B运动,若P、Q两点能相遇,求点Q的运动速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市电力部门对居民用电按月收费,标准如下:①用电不超过
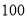 度的,每度收费
度的,每度收费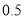 元;②用电超过
元;②用电超过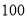 度的,超过部分每度收费
度的,超过部分每度收费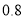 元.请根据上述收费标准解答下列问题:
元.请根据上述收费标准解答下列问题:(1)小明家
 月份用电
月份用电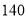 度,应交电费______________元;
度,应交电费______________元;(2)小明家
 月交电费
月交电费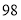 元,则他家
元,则他家 月份用电多少度?
月份用电多少度?
相关试题

