【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=80°.
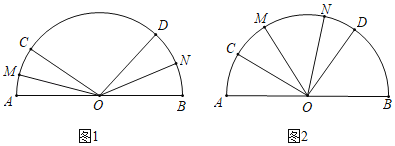
(1)如图1,OM平分∠AOC,ON平分∠BOD,求∠MON的度数;
(2)如图2,若∠AOC=x°,OM平分∠AOD,ON平分∠BOC,求∠MON的度数.
参考答案:
【答案】(1)130°;(2)50°
【解析】
(1)如图1,利用角平分线的定义得到∠MOC=![]() ∠AOC,∠NOD=
∠AOC,∠NOD=![]() ∠BOD,而∠AOC+∠BOD=100°,然后计算∠COD+∠MOC+∠NOD即可;
∠BOD,而∠AOC+∠BOD=100°,然后计算∠COD+∠MOC+∠NOD即可;
(2)如图2,利用∠AOC=x°得到∠AOD=x°+80°,∠BOD=100°﹣x°,根据角平分线的定义得到∠AOM=![]() x°+40°;∠BON=
x°+40°;∠BON=![]() ∠BOC=90°﹣
∠BOC=90°﹣![]() x°,然后利用∠MON=180°﹣(∠AOM+∠BON)进行计算即可.
x°,然后利用∠MON=180°﹣(∠AOM+∠BON)进行计算即可.
(1)如图1,
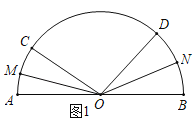
∵OM平分∠AOC,ON平分∠BOD,
∴∠MOC=![]() ∠AOC,∠NOD=
∠AOC,∠NOD=![]() ∠BOD,
∠BOD,
又∵∠COD=80°,
∴∠AOC+∠BOD=100°﹣80°=100°,
∴∠MON=∠COD+∠MOC+∠NOD=80°+![]() ×100°=130°;
×100°=130°;
(2)如图2,∠AOC=x°,则∠AOD=x°+80°,∠BOD=100°﹣x°,
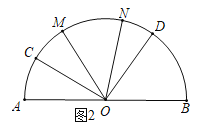
∵OM平分∠AOD
∴∠AOM=![]() ∠AOD=
∠AOD=![]() x°+40°;
x°+40°;
又∵ON平分∠BOC
∴∠BON=![]() ∠BOC=
∠BOC=![]() (180°﹣x°)=90°﹣
(180°﹣x°)=90°﹣![]() x°,
x°,
∴∠MON=180°﹣(∠AOM+∠BON)=180°﹣(![]() x°+40°+90°﹣
x°+40°+90°﹣![]() x°)
x°)
=180°﹣130°
=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】温度通常有两种表示方法:华氏度(单位:
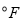 )与摄氏度(单位:
)与摄氏度(单位: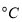 ).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.
).已知华氏度数y与摄氏度数x之间是一次函数关系.下表列出了部分华氏度与摄氏度之间的对应关系.摄氏度数x(
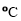 )
)…
0
…
35
…
100
…
华氏度数y(
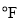 )
)…
32
…
95
…
212
…
(1)选用表格中给出的数据,求y关于x的函数解析式(不需要写出该函数的定义域);
(2)已知某天的最低气温是
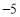
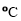 ,求与之对应的华氏度数.
,求与之对应的华氏度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠AOB=80°,∠BOC=20°,OE平分∠AOC,则∠AOE=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
注入水的时间t(分钟)
0
10
…
25
水池的容积V(公升)
100
300
…
600
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,图2,分别是吊车在吊一物品时的实物图与示意图,已知吊车底盘CD的高度为1.8米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为80°,吊臂AC与地面成70°角,求吊车的吊臂顶端A点距地面的高度是多少米?(精确到0.1米,参考数据:sin10°=cos80°=0.17,cos10°=sin80°=0.98,sin20°=cos70°=0.34,tan70°=2.75,sin70°=0.94)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=ax2+2ax﹣4(a≠0)的图象与x轴交于点A,B(A点在B点的左侧),与y轴交于点C,△ABC的面积为12.
(1)求二次函数图象的对称轴与它的解析式;
(2)点D在y轴上,当以A、O、D为顶点的三角形与△BOC相似时,求点D的坐标;
(3)点D的坐标为(﹣2,1),点P在二次函数图象上,∠ADP为锐角,且tan∠ADP=2,求点P的横坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A和B在数轴上对应的数分别为a和b,且(a+5)2+|b﹣4|=0.
(1)求线段AB的长;
(2)点C在数轴上所对应的数为x,且x是方程x﹣3=
 x﹣1的解,在线段BC上是否存在点D,使得AD+BD=
x﹣1的解,在线段BC上是否存在点D,使得AD+BD=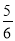 CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;
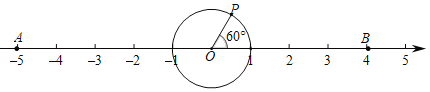
CD?若存在,请求出点D在数轴上所对应的数,若不存在,请说明理由;(3)如图,PO=1,点P在AB的上方,且∠POB=60°,点P绕着点O以30度/秒的速度在圆周上顺时针旋转一周停止,同时点Q沿线段AB自点A向点B运动,若P、Q两点能相遇,求点Q的运动速度.
相关试题

