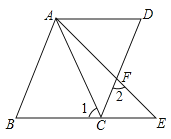
【题目】已知AD∥BE,∠B=∠D.
(1)求证:AB∥CD;
(2)若∠1=∠2=60°,∠BAC=3∠EAC,求∠DCE的度数.
参考答案:
【答案】(1)见解析;(2)75°
【解析】
(1)根据平行线的性质和判定解答即可;
(2)根据平行线的性质得到∠BAC+∠CAE=60°,设∠CAE=x,∠DAE=y,根据题意得到二元一次方程组求出x,y即可求解.
(1)∵AD∥BE,
∴∠D=∠DCE,
∵∠B=∠D,
∴∠DCE=∠B,
∴AB∥CD,
(2)∵AD∥BE,∠1=60°,
∴∠CAE+∠DAE=60°,
∵AB∥CD,∠2=60°,
∴∠BAC+∠CAE=60°,
∵∠BAC=3∠EAC,
设∠CAE=x,∠DAE=y,
可得:![]() ,
,
解得:![]() ,
,
即∠CAE=15°,∠DAE=45°,
∴∠D=180°60°45°=75°,
∴∠DCE=75°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点A,B,C,D分别在l1,l2,l3,l4上,过点D作DE⊥l1于点E,已知相邻两条平行线之间的距离为1,求AE及正方形ABCD的边长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5
 cm,且tan∠EFC=
cm,且tan∠EFC=  ,则矩形ABCD的周长是 .
,则矩形ABCD的周长是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(1)证明:四边形CFAE为菱形;
(2)连接EF交AC于点O,若BC=10,求线段OF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是根据对初一(1)班的50名同学平时最爱吃的食物的种类进行的问卷调查绘制成的统计表,请填满缺少的项并回答后面的问题.
肉类
蔬菜类
瓜果类
水产类
男生
22
1
2
女生
4
5
3
频率
64%
14%
12%
(1)选择适当的统计图表示男生平时最爱吃的食物的种类情况;
(2)就给出的初一(1)班的同学平时最爱吃的食物的种类情况,请你结合自己的年龄特点简略谈谈自己的看法.
-
科目: 来源: 题型:
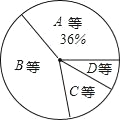
查看答案和解析>>【题目】某校为了解九年级学生的身体素质情况,体育老师对九(1)班50位学生进行测试,根据测试评分标准,将他们的得分进行统计后分为A,B,C,D四等,并绘制成如图所示的频数分布表和扇形统计图.
等第
成绩(得分)
频数(人数)
频率
A
10分
7
0.14
9分
x
m
B
8分
15
0.30
7分
8
0.16
C
6分
4
0.08
5分
y
n
5分以下
3
0.06
合计
50
1
(1)直接写出:m,x,y;
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有700名学生,试估计这700名学生中成绩达到A等和B等的人数共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的高BD与CE相交于点O,OD=OE,AO的延长线交BC于点M,请你从图中找出几对全等的直角三角形,并说明理由.

相关试题

